X 3 2x 2 3x
gasmanvison
Sep 14, 2025 · 5 min read
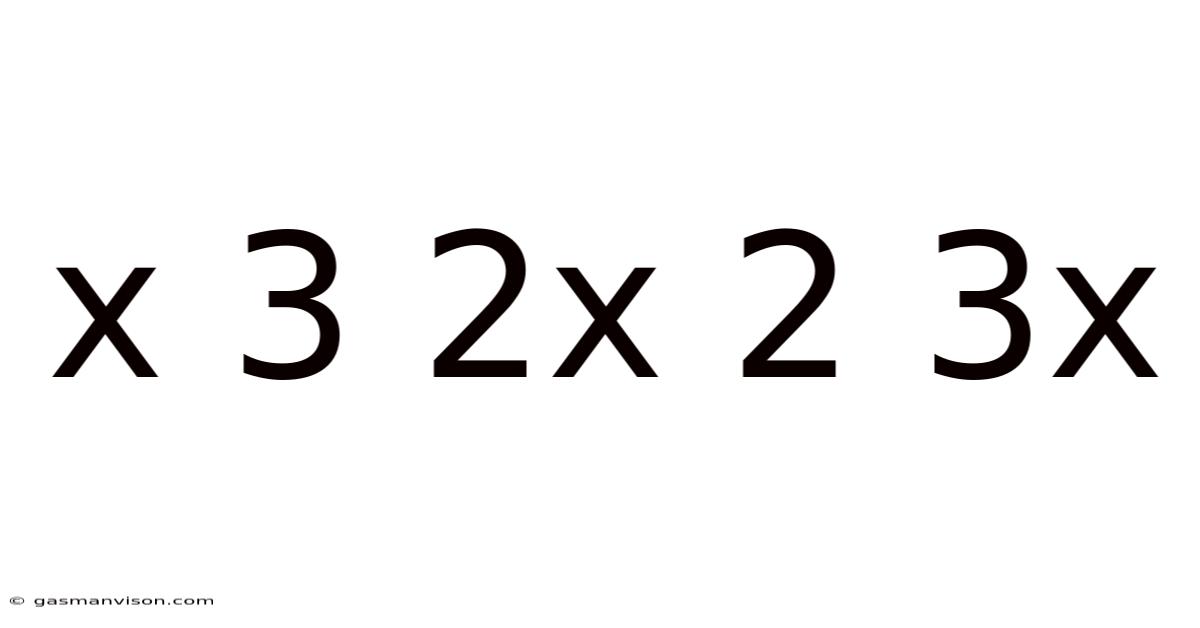
Table of Contents
Deconstructing the Mathematical Sequence: x 3 2x 2 3x – Unveiling Patterns and Possibilities
This article delves into the intriguing mathematical sequence represented by "x 3 2x 2 3x," exploring its potential interpretations, underlying patterns, and the broader mathematical concepts it touches upon. We'll analyze different approaches to understanding this sequence, considering the possibility of missing terms, hidden operations, and various mathematical frameworks that might explain its structure. This exploration aims to provide a comprehensive understanding of the sequence, catering to both those with a basic mathematical background and those seeking a deeper, more analytical perspective.
Understanding the Sequence: Initial Observations
At first glance, "x 3 2x 2 3x" appears simple. It presents a sequence of terms involving the variable 'x' and constants. The immediate challenge lies in identifying the pattern or rule governing the sequence's progression. Is it an arithmetic sequence, a geometric sequence, or does it follow a more complex, recursive relationship? The presence of both 'x' and numerical constants suggests a potentially rich mathematical structure. This initial ambiguity is precisely what makes this sequence so intriguing and worthy of investigation.
A key aspect to consider is the potential for missing terms. The sequence, as presented, could be a simplified representation of a larger, more intricate pattern. Perhaps additional terms, involving higher powers of 'x' or different constant values, are missing. Exploring this possibility requires careful consideration of various mathematical functions and their properties.
Possible Interpretations and Mathematical Frameworks
Let's explore several potential interpretations of this sequence, considering various mathematical frameworks.
1. Arithmetic Progression Hypothesis: A simple approach is to examine whether the sequence fits an arithmetic progression (AP). In an AP, the difference between consecutive terms remains constant. However, the presence of 'x' complicates this assessment. Without a specific value assigned to 'x', we cannot determine if a constant difference exists. For instance, if x = 1, the sequence becomes 1, 3, 2, 2, 3, resulting in variable differences between terms.
2. Geometric Progression Hypothesis: Similarly, a geometric progression (GP) involves a constant ratio between consecutive terms. This hypothesis also faces the same challenge as the AP hypothesis. The presence of 'x' and varying numerical constants prevents us from identifying a constant ratio between consecutive terms.
3. Recursive Sequence Hypothesis: A more flexible approach involves exploring recursive sequences. A recursive sequence defines each term based on preceding terms. We could hypothesize a recursive relation where each term depends on the previous one or a combination of previous terms. This approach offers greater flexibility in potentially explaining the observed pattern. Finding the specific recursive rule would require a trial-and-error approach or more sophisticated mathematical techniques.
4. Polynomial Representation: Another promising avenue is to consider the sequence as a representation of a polynomial function. Polynomial functions are defined by sums of powers of a variable (in this case, 'x'), multiplied by coefficients. We can attempt to fit the sequence to a polynomial of a certain degree. This requires solving a system of equations, using the given terms as constraints. Finding a polynomial that exactly fits the sequence would provide a clear mathematical model for generating additional terms.
5. Piecewise Function Hypothesis: The sequence could be interpreted as a piecewise function – a function defined by different sub-functions over different intervals. This would allow for the seemingly disparate terms to fit a coherent structure. However, without further information or context, it’s difficult to define the specific intervals and sub-functions.
Exploring the Role of 'x'
The variable 'x' plays a crucial role in the ambiguity of the sequence. Its presence suggests that the sequence might represent a more general pattern applicable to a range of values. Understanding the role of 'x' requires considering its possible interpretations:
- x as a parameter: 'x' could be a parameter controlling the sequence's overall shape or behavior. Different values of 'x' might result in entirely different sequences.
- x as a variable within a function: 'x' could be a variable within a larger function that generates the sequence. This would require identifying the function that produces the observed terms.
- x as an index: 'x' might even represent an index or position within a more complex multi-dimensional structure.
Expanding the Sequence: Hypothetical Extensions
Without a definitive rule, we can explore potential extensions to the sequence. If we assume a polynomial representation, for example, we can try fitting a polynomial to the known terms and then extrapolate to find subsequent terms. Similarly, a recursive relation could be extrapolated to generate additional terms. These extensions, however, would remain hypothetical until a definitive rule is established.
Let's consider a few possibilities:
-
Extension 1 (Linear Pattern Assumption): If we assume a simplistic linear pattern, albeit unlikely, the sequence could be extended in various ways. We lack enough data to derive a conclusive trend.
-
Extension 2 (Quadratic Pattern Assumption): A quadratic function might fit the existing data points, yet the absence of a pattern makes it difficult to confidently extrapolate a sequence.
-
Extension 3 (Recursive Approach): A recursive rule could be postulated and used to extend the sequence. However, several recursive rules could theoretically accommodate the provided data points.
The Importance of Context
The interpretation of the sequence heavily depends on its context. Where did this sequence originate? What is the broader problem or puzzle it's a part of? Knowing the source of the sequence could provide vital clues about its intended meaning and the underlying mathematical relationships. Without context, we are left with many plausible, but ultimately unsubstantiated, interpretations.
Conclusion: The Open-Ended Nature of the Problem
The sequence "x 3 2x 2 3x" poses a fascinating challenge, highlighting the ambiguity and open-ended nature of mathematical problem-solving. The absence of a clear pattern or context allows for multiple valid interpretations. The investigation has shown the importance of considering various mathematical tools and frameworks, from simple arithmetic and geometric progressions to more complex recursive relations and polynomial representations. Ultimately, the true meaning of the sequence remains elusive without further information or a clearly stated problem context. The exercise, however, underscores the richness and complexity inherent in mathematical sequences and the creativity involved in deciphering their underlying patterns. Further investigation, perhaps incorporating more data points or specifying the context of the sequence, could lead to a more definitive understanding.
Latest Posts
Latest Posts
-
Molecular Mass Of Magnesium Hydroxide
Sep 14, 2025
-
Charles Bonnet Syndrome Icd 10
Sep 14, 2025
-
Nitric Oxide Vs Nitrous Oxide
Sep 14, 2025
-
This Citation Is Missing The
Sep 14, 2025
-
Identity Vs Role Confusion Example
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about X 3 2x 2 3x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.