X Squared Plus X Squared
gasmanvison
Sep 02, 2025 · 5 min read
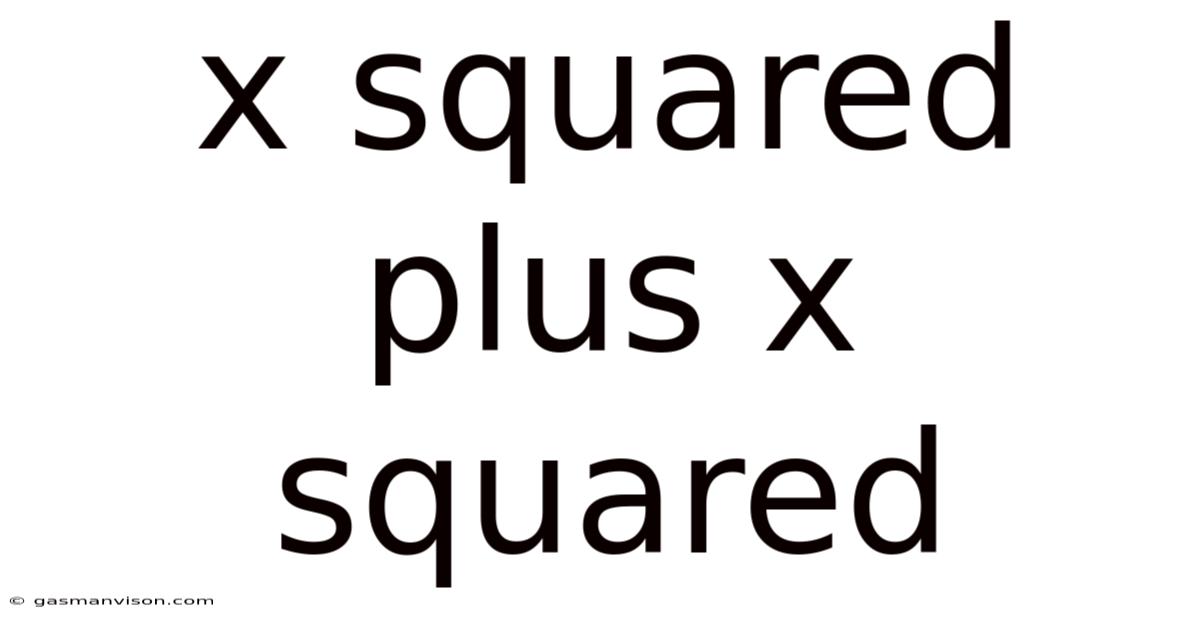
Table of Contents
Decoding x² + x²: A Deep Dive into Algebraic Simplification and its Applications
This article delves into the seemingly simple algebraic expression, x² + x², exploring its simplification, practical applications, and the broader mathematical concepts it embodies. While the answer may appear immediately obvious to many, understanding the underlying principles is crucial for grasping more complex algebraic manipulations and their use in various fields. This comprehensive guide will cater to both beginners seeking a foundational understanding and more advanced learners looking to solidify their grasp of algebraic fundamentals.
What is x² + x²?
At its core, x² + x² represents the sum of two identical terms: x squared. The solution is straightforward: 2x². This simplification stems from the basic principle of combining like terms in algebra. Like terms are terms that have the same variables raised to the same powers. In this case, both terms are x², making them like terms, thus allowing for direct addition of their coefficients (which are both implicitly 1).
This seemingly basic equation forms the bedrock for numerous more complex algebraic manipulations. Mastering its simplification is essential before tackling problems involving higher powers, multiple variables, and more intricate algebraic expressions.
Understanding the Fundamentals: Variables, Exponents, and Coefficients
Before delving deeper into applications, let's review some fundamental algebraic concepts:
-
Variables: A variable, typically represented by a letter (like 'x' in our example), represents an unknown or unspecified numerical value. It can take on different values depending on the context.
-
Exponents: The exponent (the small number written above and to the right of the variable) indicates how many times the variable is multiplied by itself. In x², the exponent is 2, meaning x is multiplied by itself (x * x).
-
Coefficients: The coefficient is the numerical factor that multiplies the variable. In x², the coefficient is 1 (implicitly, as 1*x² = x²). In 2x², the coefficient is 2.
Understanding these core concepts allows for a more profound comprehension of why x² + x² simplifies to 2x². We are essentially adding the coefficients (1 + 1) while keeping the variable and its exponent unchanged.
Beyond Simple Addition: Applications of x² + x² and its Extensions
While the simplification of x² + x² appears elementary, its application extends far beyond simple algebraic exercises. Understanding this basic principle forms the foundation for more complex mathematical operations and is instrumental across various disciplines:
1. Geometry and Area Calculations:
Imagine two squares with side lengths of 'x'. The area of each square is x². The combined area of these two squares is x² + x², which simplifies to 2x². This simple example illustrates how the expression relates to geometric concepts and provides a visual representation of algebraic addition. This concept extends to more complex shapes and area calculations involving multiple squares or other geometric figures with sides expressed as algebraic expressions.
2. Physics and Quadratic Equations:
Many physical phenomena are modeled using quadratic equations, which often involve terms like x². The expression x² + x² might represent, for instance, the combined distance traveled by two objects moving independently with displacement functions involving x². Solving such equations relies heavily on the ability to manipulate and simplify algebraic expressions, starting with the fundamentals like combining like terms.
3. Calculus and Derivatives:
In calculus, finding the derivative of a function often involves simplifying algebraic expressions. If we encounter a function that includes a term like x² + x², we must simplify it to 2x² before proceeding with differentiation. This basic simplification lays the groundwork for understanding more complex differentiation processes involving polynomials and other functions.
4. Financial Modeling and Compound Interest:
Compound interest calculations often involve exponential growth, represented by equations containing squared and higher-order terms. While not directly represented by x² + x², the principle of combining like terms, as demonstrated in this simple equation, is crucial in manipulating complex financial formulas and forecasting future values.
5. Computer Science and Algorithm Optimization:
In computer science, optimizing algorithms often requires analyzing time and space complexity. Simplified algebraic expressions help in analyzing the efficiency of algorithms. Although not directly applying x² + x², the underlying concept of simplifying expressions is paramount in algorithmic analysis and optimization.
6. Engineering and Design:
Engineering designs frequently involve calculations involving areas, volumes, and other physical quantities represented by algebraic expressions. Simplifying these expressions is crucial for accurate calculations and efficient design optimization. The ability to combine like terms smoothly and swiftly is an essential skill for engineers of all disciplines.
Extending the Concept: More Complex Expressions
The principle of combining like terms extends to more complex algebraic expressions involving multiple variables and higher powers. For example:
- 2x² + 3x² = 5x² (Adding coefficients of like terms)
- x²y + 2x²y = 3x²y (Adding coefficients of like terms with multiple variables)
- 3x³ + x³ = 4x³ (Adding coefficients of like terms with higher powers)
These examples illustrate how the core principle of combining like terms remains constant, regardless of the complexity of the expression. The ability to seamlessly simplify these expressions is a critical skill for any student of mathematics or related fields.
Mistakes to Avoid:
While seemingly straightforward, several common mistakes can arise when dealing with algebraic expressions:
-
Adding unlike terms: A common error is attempting to add terms that are not like terms. For example, x² + x ≠ 2x². These terms have different exponents and therefore cannot be directly combined.
-
Incorrect exponent manipulation: Incorrectly handling exponents leads to errors in simplification. Remember, adding terms does not change the exponent; only the coefficient is affected when adding like terms.
-
Neglecting negative signs: When dealing with negative coefficients, carefully account for the signs during addition or subtraction. For instance, 3x² - x² = 2x², not 4x².
Conclusion:
The seemingly simple expression x² + x² = 2x² serves as a fundamental building block in algebra and various other disciplines. Mastering its simplification allows for a more profound understanding of algebraic manipulation and its extensive applications in geometry, physics, calculus, finance, computer science, and engineering. The principles of combining like terms and handling variables, exponents, and coefficients correctly are crucial for navigating more complex algebraic problems and solving real-world mathematical challenges. The consistent practice and thorough understanding of these foundational concepts are key to success in advanced mathematics and related fields. This in-depth examination reveals that even the simplest algebraic concepts hold significant weight and application in the wider world of mathematics and beyond.
Latest Posts
Latest Posts
-
What Is 25 Of 200 00
Sep 03, 2025
-
What Does A Cytoplasm Do
Sep 03, 2025
-
I Am The In Spanish
Sep 03, 2025
-
Bookmarked Here For Unread Messages
Sep 03, 2025
-
Equivalent Fractions For 2 5
Sep 03, 2025
Related Post
Thank you for visiting our website which covers about X Squared Plus X Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.