X2 + X + 36
gasmanvison
Sep 09, 2025 · 5 min read
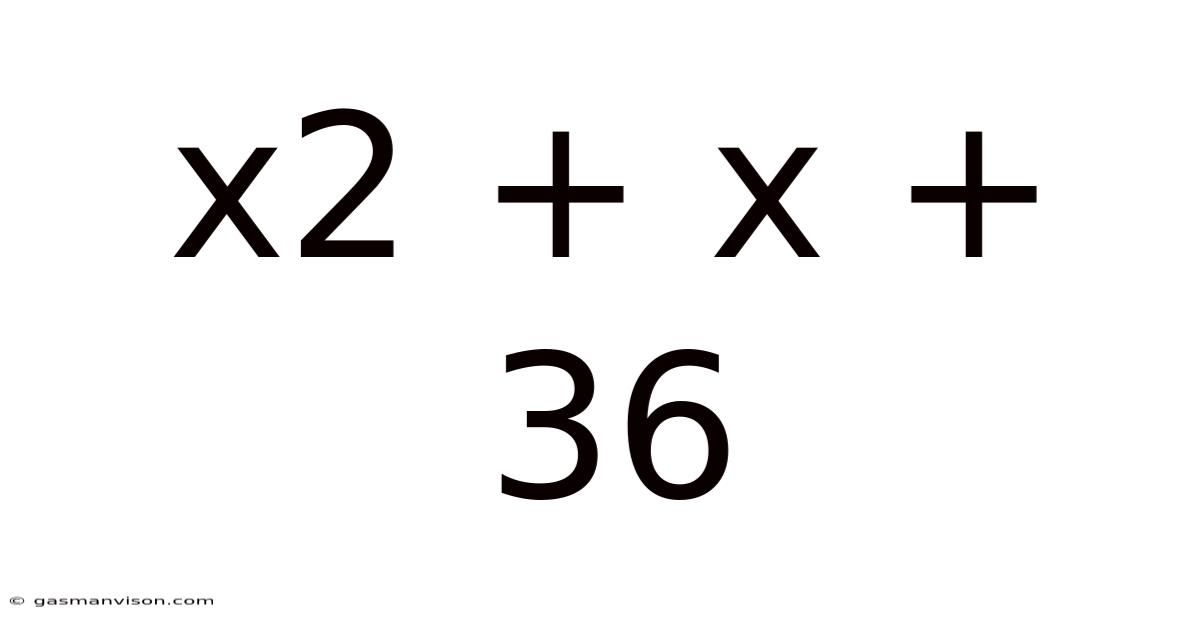
Table of Contents
Exploring the Quadratic Expression x² + x + 36: A Deep Dive into its Properties and Applications
This article delves into the quadratic expression x² + x + 36, exploring its various properties, potential applications, and the mathematical concepts surrounding it. We'll analyze its roots, discriminant, graph, and discuss how understanding such expressions is crucial in various fields like physics, engineering, and computer science. This comprehensive guide aims to provide a thorough understanding of this seemingly simple yet mathematically rich expression.
Understanding Quadratic Expressions
Before we dive into the specifics of x² + x + 36, let's establish a foundational understanding of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (in this case, x) is 2. The general form of a quadratic expression is ax² + bx + c, where a, b, and c are constants, and 'a' is not equal to zero. Our expression, x² + x + 36, fits this form perfectly, with a = 1, b = 1, and c = 36.
Finding the Roots (Solutions) of x² + x + 36
The roots of a quadratic expression are the values of x that make the expression equal to zero. We find these roots by solving the quadratic equation: x² + x + 36 = 0. There are several methods to solve quadratic equations, including factoring, completing the square, and using the quadratic formula. Let's explore the most common method: the quadratic formula.
The quadratic formula is given by:
x = [-b ± √(b² - 4ac)] / 2a
Plugging in the values from our expression (a = 1, b = 1, c = 36), we get:
x = [-1 ± √(1² - 4 * 1 * 36)] / 2 * 1
x = [-1 ± √(1 - 144)] / 2
x = [-1 ± √(-143)] / 2
Notice that we have a negative number under the square root. This signifies that the roots of the quadratic equation x² + x + 36 = 0 are complex numbers, not real numbers. Complex numbers involve the imaginary unit 'i', where i² = -1. Therefore, the roots are:
x = [-1 ± i√143] / 2
This means the expression x² + x + 36 does not intersect the x-axis when graphed on a Cartesian plane.
The Discriminant and its Significance
The expression b² - 4ac within the quadratic formula is called the discriminant. It provides valuable information about the nature of the roots of a quadratic equation:
- Discriminant > 0: Two distinct real roots. The parabola intersects the x-axis at two points.
- Discriminant = 0: One real root (a repeated root). The parabola touches the x-axis at one point.
- Discriminant < 0: Two complex roots (conjugate pairs). The parabola does not intersect the x-axis.
In our case, the discriminant is 1 - 144 = -143, which is less than 0. This confirms our earlier finding that the roots are complex numbers.
Graphing the Quadratic Expression
Graphing the quadratic expression x² + x + 36 helps visualize its behavior. The graph of a quadratic expression is a parabola. Since the coefficient of x² (a = 1) is positive, the parabola opens upwards. The vertex of the parabola represents the minimum value of the expression. The x-coordinate of the vertex is given by -b/2a = -1/2. Substituting this into the expression gives us the y-coordinate: (-1/2)² + (-1/2) + 36 = 35.75. Therefore, the vertex is at (-0.5, 35.75). The parabola lies entirely above the x-axis, reflecting the fact that there are no real roots.
Applications of Quadratic Expressions
Quadratic expressions and equations have numerous applications across various fields:
-
Physics: Projectile motion, where the trajectory of a projectile follows a parabolic path, is described by quadratic equations. Understanding quadratic expressions is essential for calculating the maximum height, range, and time of flight of projectiles.
-
Engineering: Quadratic equations are used in structural design to calculate stresses and strains in beams and other structural elements. They also appear in the design of bridges, buildings, and other infrastructure projects.
-
Computer Science: Quadratic equations are used in algorithms and data structures, such as finding the optimal solution in certain optimization problems.
-
Economics: Quadratic functions can model cost, revenue, and profit functions in economics, helping to determine optimal production levels and pricing strategies.
-
Mathematics itself: Quadratic equations are fundamental building blocks in more advanced mathematical concepts, like calculus and linear algebra.
Completing the Square for x² + x + 36
Another method to solve quadratic equations is completing the square. This technique involves manipulating the equation to create a perfect square trinomial. Let's apply this to our expression:
x² + x + 36 = 0
First, move the constant term to the right side:
x² + x = -36
Next, take half of the coefficient of x (which is 1), square it (1/4), and add it to both sides:
x² + x + 1/4 = -36 + 1/4
Now, the left side is a perfect square trinomial:
(x + 1/2)² = -143/4
Taking the square root of both sides:
x + 1/2 = ±i√143/2
Solving for x:
x = -1/2 ± i√143/2
This confirms the complex roots we obtained using the quadratic formula.
Further Exploration and Related Concepts
The exploration of x² + x + 36 opens doors to several related mathematical concepts:
-
Complex Numbers: A deeper understanding of complex numbers, their properties, and their representation in the complex plane is essential for fully grasping the nature of the roots of this quadratic expression.
-
Parabolas and Conic Sections: Studying the properties of parabolas, including their focus, directrix, and axis of symmetry, provides a more complete picture of the graphical representation of the expression.
-
Polynomial Equations of Higher Degree: Understanding quadratic expressions provides a foundation for tackling polynomial equations of higher degrees, which involve more complex solutions and techniques.
Conclusion
While seemingly simple, the quadratic expression x² + x + 36 offers a rich tapestry of mathematical concepts and applications. From its complex roots and upward-opening parabola to its relevance in various scientific and engineering fields, this expression showcases the power and versatility of quadratic equations. This in-depth analysis highlights the importance of understanding the fundamental principles of algebra and their broader implications in diverse areas of study and application. The journey from a simple expression to a deeper understanding of complex numbers and parabolic functions demonstrates the beauty and interconnectedness of mathematics. Further exploration into these related concepts will undoubtedly enhance your mathematical prowess and appreciation for the elegance of quadratic expressions.
Latest Posts
Latest Posts
-
What Was The Mita System
Sep 09, 2025
-
What Party Was George Washington
Sep 09, 2025
-
4 45 Repeating As A Fraction
Sep 09, 2025
-
Is A Quart 32 Ounces
Sep 09, 2025
-
A Smart Refrigerator Can Use
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about X2 + X + 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.