Y Mx B For X
gasmanvison
Sep 11, 2025 · 5 min read
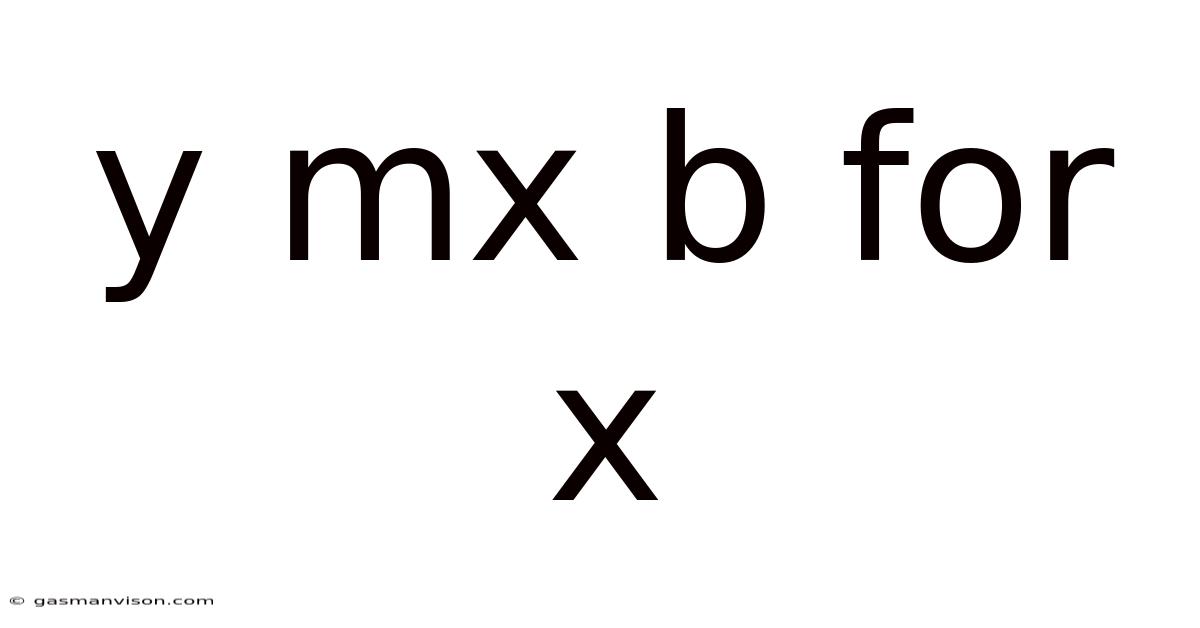
Table of Contents
Solving for x in y = mx + b: A Comprehensive Guide
This article provides a thorough explanation of how to solve for x in the equation of a straight line, y = mx + b. Understanding this fundamental algebraic manipulation is crucial for various mathematical applications, from simple geometry problems to advanced calculus concepts. We'll explore different scenarios, offering step-by-step solutions and practical examples to solidify your understanding. This guide will cover solving for x when y, m, and b are known, as well as situations where one or more of these variables are unknown or represented by expressions.
What is y = mx + b?
The equation y = mx + b represents a straight line on a Cartesian coordinate plane. It's a cornerstone of algebra and serves as the foundation for many higher-level mathematical concepts. Let's break down the meaning of each variable:
- y: Represents the y-coordinate of any point on the line.
- x: Represents the x-coordinate of any point on the line.
- m: Represents the slope of the line, which indicates the steepness and direction of the line. A positive slope indicates an upward trend, while a negative slope indicates a downward trend. A slope of zero indicates a horizontal line.
- b: Represents the y-intercept, which is the y-coordinate of the point where the line intersects the y-axis (where x = 0).
Solving for x when y, m, and b are known
This is the most straightforward scenario. The process involves isolating x on one side of the equation through a series of algebraic manipulations. Here's a step-by-step guide:
-
Start with the equation: y = mx + b
-
Subtract 'b' from both sides: y - b = mx
-
Divide both sides by 'm': (y - b) / m = x
-
Therefore, the solution for x is: x = (y - b) / m
Example:
Let's say we have the equation y = 2x + 3, and we want to find the x-coordinate when y = 7. We can substitute the known values into the formula:
x = (7 - 3) / 2 = 2
Therefore, when y = 7, x = 2. This point (2, 7) lies on the line y = 2x + 3.
Handling scenarios with unknown or expression-based variables
Solving for x becomes slightly more complex when one or more of the variables (y, m, or b) are unknown or represented by algebraic expressions. Let's explore these scenarios:
1. Unknown 'y'
If 'y' is unknown, the solution for x will be an expression in terms of 'y'. You cannot find a numerical value for x without knowing the value of 'y'. The solution remains:
x = (y - b) / m
Example:
If the equation is y = 3x + 5, and 'y' is unknown, the solution for 'x' in terms of 'y' is:
x = (y - 5) / 3
2. Unknown 'm'
Similarly, if 'm' is unknown, the solution for x will be an expression in terms of 'm'. You cannot solve for a numerical value for x without knowing 'm'. The solution will be:
x = (y - b) / m
Example:
Given y = mx + 2, and 'm' is unknown, the solution for 'x' in terms of 'm' is:
x = (y - 2) / m
3. Unknown 'b'
If 'b' is unknown, the solution for x will be an expression in terms of 'b'. Again, a numerical value for x cannot be obtained without knowing 'b'. The solution is:
x = (y - b) / m
Example:
Given y = 4x + b, and 'b' is unknown, the solution for 'x' in terms of 'b' is:
x = (y - b) / 4
4. Expression-based variables
The complexity increases when one or more variables are represented by algebraic expressions. The process remains the same; substitute the expressions and then simplify the resulting equation to solve for x.
Example:
Let's say we have the equation y = (2a + 1)x + 3a, where 'a' is a constant. We want to solve for x when y = 7a + 4.
-
Substitute the known values: 7a + 4 = (2a + 1)x + 3a
-
Subtract 3a from both sides: 4a + 4 = (2a + 1)x
-
Divide both sides by (2a + 1): x = (4a + 4) / (2a + 1)
This gives the solution for x in terms of the constant 'a'.
Applications of Solving for x in y = mx + b
The ability to solve for x in y = mx + b has widespread applications in various fields:
- Geometry: Finding the x-coordinate of intersection points between lines.
- Physics: Calculating the time taken for an object to reach a certain position given its velocity and initial position (represented by the slope and y-intercept respectively).
- Economics: Determining the quantity demanded or supplied given a linear demand or supply function.
- Computer Graphics: Defining and manipulating lines and points in two-dimensional space.
- Data Analysis: Predicting values based on linear regression models.
Advanced Scenarios and Considerations
While the basic method of solving for x is straightforward, certain scenarios require more advanced techniques:
- Systems of Linear Equations: When dealing with multiple linear equations, methods such as substitution or elimination are used to find the values of both x and y.
- Simultaneous Equations: Solving for x and y requires considering both equations simultaneously.
- Non-linear Equations: If the equation isn't linear (e.g., contains squared terms or other non-linear functions), solving for x may require more sophisticated algebraic techniques or numerical methods.
Conclusion
Solving for x in the equation y = mx + b is a fundamental algebraic skill with far-reaching applications. Understanding the process and its variations, from simple scenarios to those involving expressions and simultaneous equations, is essential for success in mathematics and related fields. By mastering this technique, you'll enhance your problem-solving abilities and open up a world of mathematical possibilities. Remember to practice regularly to build your confidence and speed in solving these types of problems. Through consistent practice and application, this seemingly simple equation will become a powerful tool in your mathematical arsenal.
Latest Posts
Latest Posts
-
How Are Unlike Fractions Identified
Sep 11, 2025
-
Economic Characteristics Of Land Include
Sep 11, 2025
-
Solid Abdominal Organs Include The
Sep 11, 2025
-
Core Connections Course 3 Answers
Sep 11, 2025
-
Spanish Vs Mestizo Vs Indigenous
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Y Mx B For X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.