1 2 6 24 120
gasmanvison
Sep 03, 2025 · 5 min read
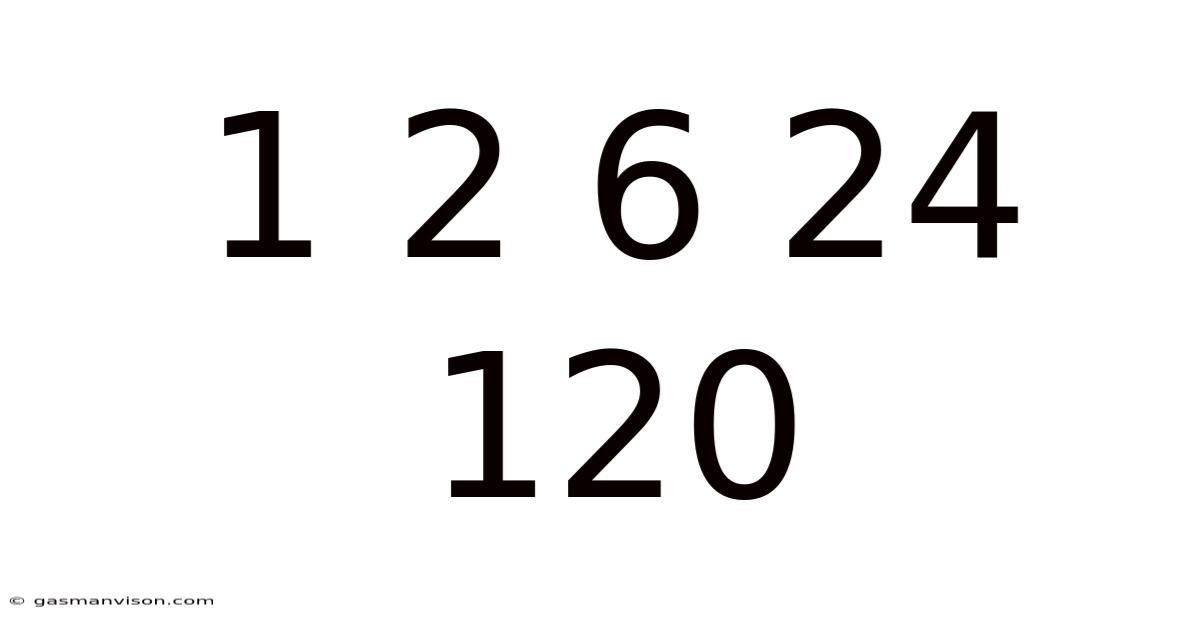
Table of Contents
Decoding the Sequence: Unveiling the Secrets of 1, 2, 6, 24, 120
This seemingly simple sequence, 1, 2, 6, 24, 120, holds a fascinating mathematical secret. At first glance, it might seem arbitrary, but a closer inspection reveals a beautiful pattern based on a fundamental mathematical concept: factorials. This article will delve deep into this sequence, exploring its underlying structure, its connection to factorials, its applications in various fields, and its potential for further mathematical exploration. Understanding this sequence offers a gateway to appreciating the elegance and power of mathematical relationships. We'll explore its generation, its properties, and its surprising relevance beyond simple numerical patterns.
What are Factorials?
Before we unravel the mystery of the sequence, let's define the key concept: the factorial. A factorial, denoted by an exclamation mark (!), is the product of all positive integers less than or equal to a given positive integer. For example:
- 1! = 1
- 2! = 2 × 1 = 2
- 3! = 3 × 2 × 1 = 6
- 4! = 4 × 3 × 2 × 1 = 24
- 5! = 5 × 4 × 3 × 2 × 1 = 120
Now, the pattern in our sequence (1, 2, 6, 24, 120) becomes strikingly clear. Each number in the sequence is simply the factorial of its position:
- 1st position: 1! = 1
- 2nd position: 2! = 2
- 3rd position: 3! = 6
- 4th position: 4! = 24
- 5th position: 5! = 120
This simple yet elegant relationship forms the core of this numerical sequence. Understanding this connection is crucial to further explore its properties and applications.
Extending the Sequence: Predicting Future Values
Armed with this understanding, we can easily predict future values in the sequence. The next number would be 6!, which is 6 × 5 × 4 × 3 × 2 × 1 = 720. Similarly, the subsequent number would be 7!, and so on. This ability to extrapolate the sequence highlights the predictive power of recognizing underlying mathematical patterns. This simple pattern allows for the generation of an infinitely long sequence, simply by calculating successive factorials.
Applications of Factorials and the Sequence
While seemingly simple, factorials and sequences derived from them have far-reaching applications in various fields:
-
Combinatorics and Probability: Factorials are fundamental in combinatorics, the study of counting and arranging objects. They are used to calculate permutations (arrangements of objects where order matters) and combinations (selections of objects where order doesn't matter). For instance, calculating the number of ways to arrange a deck of cards or the probability of a specific hand in poker involves factorials. Understanding the sequence 1, 2, 6, 24, 120 provides a foundational understanding of these crucial concepts.
-
Calculus: Factorials play a crucial role in calculus, particularly in Taylor and Maclaurin series expansions. These series represent functions as infinite sums, with factorials appearing in the denominators of the terms. This allows for the approximation of complex functions using simpler polynomial expressions. The foundational understanding of factorials derived from our sequence is crucial for grasping these advanced mathematical concepts.
-
Statistics: In statistics, factorials are integral to various distributions, such as the binomial and Poisson distributions. These distributions model probabilities of events occurring a certain number of times in a given number of trials. The sequence provides a tangible entry point into understanding the underpinnings of these statistical tools.
-
Computer Science: Factorials and their related algorithms are commonly used in computer science, particularly in areas such as algorithm analysis, cryptography, and data structures. Efficient computation of factorials is a significant aspect of optimizing performance in various computational tasks. The sequence itself serves as a simple yet illustrative example of such computational patterns.
Beyond Factorials: Exploring Related Sequences
The sequence 1, 2, 6, 24, 120 is just one example of a sequence based on factorials. Numerous other sequences can be constructed by manipulating factorials or combining them with other mathematical operations. Exploring these related sequences can lead to further insights into the rich world of mathematics.
For instance, we could explore sequences based on:
-
Double Factorials: These involve the product of every other integer. For example, 5!! = 5 × 3 × 1 = 15. A sequence based on double factorials would exhibit a different, yet equally interesting, pattern.
-
Subfactorial Sequences: These relate to derangements, which are permutations where no element appears in its original position. The sequence of subfactorials demonstrates a fascinating connection between factorials and permutations with specific constraints.
-
Sequences involving Factorial Ratios: We can create sequences using ratios of factorials, leading to different growth patterns and mathematical properties.
The Sequence in Programming
The simplicity of the sequence makes it an ideal candidate for programming exercises. A simple recursive function can easily generate this sequence:
def factorial_sequence(n):
"""Generates the factorial sequence up to n terms."""
if n == 0:
return []
else:
result = [1]
fact = 1
for i in range(2, n + 1):
fact *= i
result.append(fact)
return result
print(factorial_sequence(5)) # Output: [1, 2, 6, 24, 120]
This code snippet demonstrates the straightforward computation of the sequence, highlighting the elegance of the underlying mathematical structure. It serves as a practical example of how mathematical concepts translate into concrete computational tasks.
Further Mathematical Explorations
The sequence 1, 2, 6, 24, 120 offers a springboard for further mathematical investigations. For instance:
-
Generating Functions: We can explore the generating function for this sequence, which provides a compact representation of the sequence using a power series.
-
Asymptotic Analysis: Analyzing the asymptotic behavior of the sequence (how it behaves for very large values of n) can provide insights into its growth rate and properties.
-
Relationships to Other Mathematical Concepts: Further research could explore connections between this sequence and other mathematical concepts, potentially revealing hidden relationships and new avenues of investigation.
Conclusion:
The seemingly simple sequence 1, 2, 6, 24, 120 reveals a rich tapestry of mathematical concepts, primarily centered around the notion of factorials. From its straightforward generation to its multifaceted applications across diverse fields, this sequence exemplifies the elegance and power of mathematical patterns. Its simplicity provides an accessible entry point for exploring more advanced concepts in combinatorics, calculus, statistics, and computer science. By understanding this sequence, we gain a deeper appreciation for the interconnectedness of mathematical ideas and their pervasive influence in the world around us. The sequence, therefore, acts not just as a numerical puzzle but as a key to unlocking a deeper understanding of fundamental mathematical principles and their practical applications. Further exploration of related sequences and their properties promises even richer insights into the vast and fascinating world of mathematics.
Latest Posts
Latest Posts
-
4 Divided By 1 3
Sep 05, 2025
-
Multiple Intelligence Theory Explains That
Sep 05, 2025
-
How To Cancel Brainly Subscription
Sep 05, 2025
-
Resistance Training Can Effectively Improve
Sep 05, 2025
-
What Is 25 Of 500
Sep 05, 2025
Related Post
Thank you for visiting our website which covers about 1 2 6 24 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.