4 Divided By 1 3
gasmanvison
Sep 05, 2025 · 5 min read
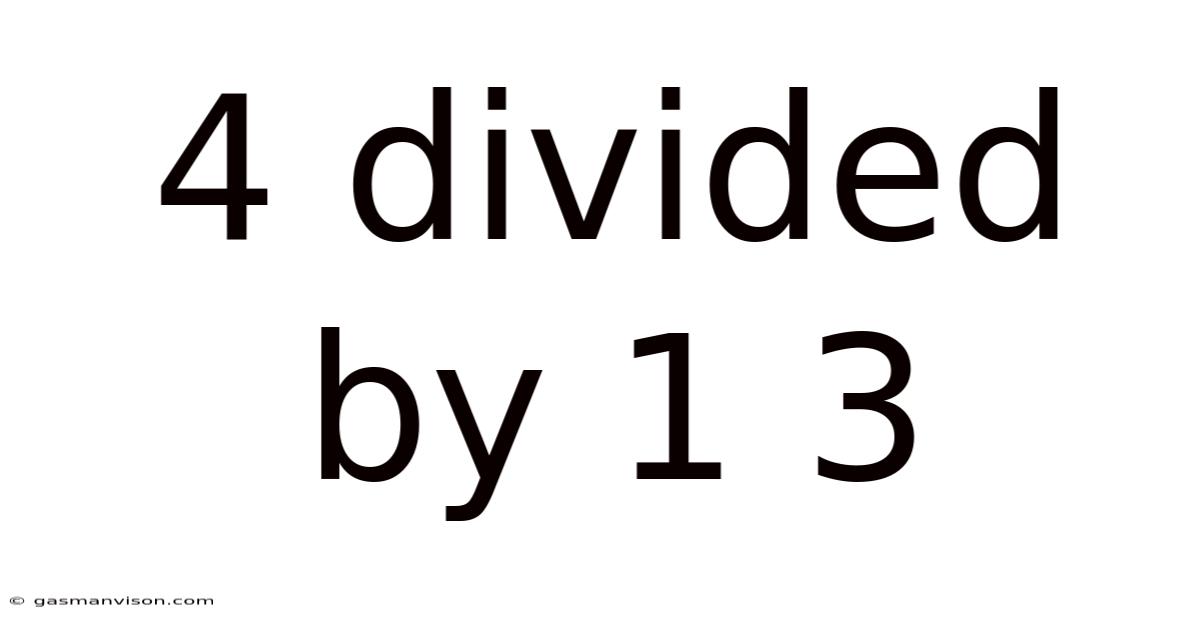
Table of Contents
Decoding 4 Divided by 1⅓: A Deep Dive into Fraction Division
The seemingly simple question, "What is 4 divided by 1⅓?", hides a surprising depth of mathematical concepts. While a calculator provides a quick answer, understanding the why behind the solution unlocks a broader appreciation for fraction manipulation and its practical applications. This article will dissect this problem, exploring different methods of solving it, connecting it to real-world scenarios, and highlighting its importance in various mathematical fields. We'll delve into the intricacies of fraction division, explore the concept of reciprocals, and illustrate how this seemingly basic operation forms the foundation for more complex calculations.
Understanding the Problem: 4 ÷ 1⅓
At its core, this problem asks: "How many times does 1⅓ fit into 4?" This phrasing immediately hints at the process of division. We're not simply looking for a numerical result; we're exploring the relationship between two quantities. Before diving into the solution methods, let's establish a crucial understanding: dividing by a fraction is equivalent to multiplying by its reciprocal.
Method 1: Converting to Improper Fractions
The most common and arguably the most straightforward method involves converting the mixed number (1⅓) into an improper fraction. This process standardizes the calculation, making it easier to perform the division.
-
Step 1: Convert 1⅓ to an improper fraction. To do this, we multiply the whole number (1) by the denominator (3), add the numerator (1), and place the result over the original denominator: (1 × 3 + 1) / 3 = 4/3.
-
Step 2: Rewrite the division problem. The problem now becomes 4 ÷ (4/3).
-
Step 3: Apply the rule of fraction division. Remember, dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of 4/3 is 3/4. Therefore, the problem transforms into 4 × (3/4).
-
Step 4: Perform the multiplication. Multiply the numerators (4 × 3 = 12) and the denominators (1 × 4 = 4). This gives us 12/4.
-
Step 5: Simplify the fraction. 12/4 simplifies to 3.
Therefore, 4 divided by 1⅓ equals 3.
Method 2: Using Decimal Equivalents
An alternative approach involves converting both numbers into decimal form. This method is particularly useful when dealing with more complex fractions or when a calculator is readily available.
-
Step 1: Convert 1⅓ to a decimal. 1⅓ is equal to 1.333... (repeating decimal).
-
Step 2: Perform the division. Divide 4 by 1.333... using a calculator or long division.
-
Step 3: Obtain the result. The result will be approximately 3. The slight discrepancy arises from the repeating decimal nature of 1⅓. Using a more precise decimal representation will yield a closer approximation to 3.
Method 3: Visual Representation – The Area Model
Visualizing the problem can be insightful, especially for those who benefit from a more concrete understanding. Imagine a rectangle with an area of 4 square units. We want to determine how many rectangles with an area of 1⅓ square units can fit inside. While not as precise as the previous methods, this approach helps solidify the concept of division as a process of finding how many times one quantity fits into another. This method requires a good understanding of area calculation and visual representation of fractions.
Real-World Applications of Fraction Division
The seemingly abstract concept of dividing by a fraction has numerous practical applications in everyday life and various professional fields:
-
Cooking and Baking: Scaling recipes up or down often involves dividing quantities by fractions. For example, if a recipe calls for 1⅓ cups of flour and you want to halve the recipe, you'll need to divide 1⅓ by 2.
-
Construction and Engineering: Precise measurements are crucial in these fields. Dividing lengths or quantities of materials often involves fractions, especially when dealing with non-standard sizes.
-
Finance and Budgeting: Allocating resources based on fractional percentages is common in financial planning and budgeting. For instance, dividing a budget among different categories according to fractional shares.
-
Science and Data Analysis: Fraction division is integral to many scientific calculations, including data analysis, where dealing with proportions and ratios is prevalent.
Expanding the Concept: Beyond 4 ÷ 1⅓
The principles illustrated using 4 ÷ 1⅓ can be extrapolated to solve more complex problems involving fraction division. The core concepts – converting to improper fractions, finding reciprocals, and performing multiplication – remain consistent.
Addressing Common Mistakes
A common mistake is incorrectly applying the rules of fraction division. Remember, we multiply by the reciprocal, not divide by the reciprocal. Another frequent error involves incorrectly converting mixed numbers to improper fractions. Careful attention to these steps is crucial for accuracy.
Conclusion: The Significance of Mastery
Mastering fraction division is not just about getting the correct answer; it's about developing a deep understanding of fundamental mathematical principles. The ability to confidently and accurately work with fractions is a cornerstone of mathematical literacy, opening doors to more advanced concepts in algebra, calculus, and beyond. The seemingly simple problem of 4 divided by 1⅓ serves as a microcosm of broader mathematical concepts, emphasizing the importance of conceptual understanding alongside computational skills. The various methods explored in this article provide a comprehensive approach to tackling such problems, allowing individuals to choose the method best suited to their understanding and the complexity of the problem at hand. By grasping the underlying principles, we can confidently navigate a wide range of mathematical challenges involving fractions and their manipulation.
Latest Posts
Latest Posts
-
What Is 25 Of 3000
Sep 05, 2025
-
1 3 X 10 4
Sep 05, 2025
-
2 Percent As A Decimal
Sep 05, 2025
-
Both Historical And Feminist Criticisms
Sep 05, 2025
-
Penny Is Conductor Or Insulator
Sep 05, 2025
Related Post
Thank you for visiting our website which covers about 4 Divided By 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.