12 Is What Of 30
gasmanvison
Sep 24, 2025 · 5 min read
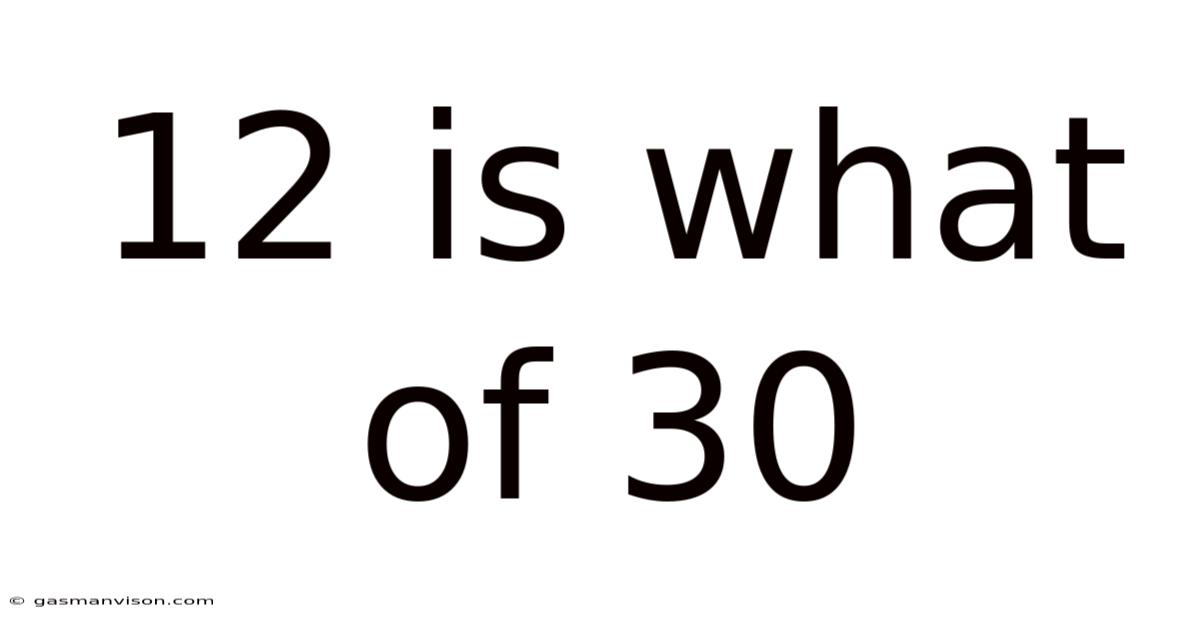
Table of Contents
12 is What Percent of 30? Understanding Percentages and Their Applications
This seemingly simple question, "12 is what percent of 30?", opens the door to a broader understanding of percentages, their calculation, and their widespread applications in various fields. This article will not only answer the question directly but also delve into the underlying mathematical principles, explore different methods of calculation, and showcase real-world examples where understanding percentages is crucial.
Meta Description: Discover how to calculate percentages, understand the concept of "12 is what percent of 30?", and explore its practical applications in everyday life and various professional fields. Learn different calculation methods and master this fundamental mathematical skill.
Understanding Percentages: A Foundation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." So, 10% means 10 out of 100, or 10/100, which simplifies to 1/10. Understanding this basic concept is essential for tackling percentage problems. In essence, percentages provide a standardized way to compare proportions and make relative comparisons easier to grasp.
Calculating Percentages: Different Approaches
There are several ways to calculate percentages, each offering a slightly different perspective and level of complexity. Let's explore the most common methods:
Method 1: The Proportion Method
This method relies on setting up a proportion. We know that "12 is what percent of 30?" can be written as a proportion:
12/30 = x/100
Where 'x' represents the unknown percentage. To solve for x, we cross-multiply:
30x = 1200
Then, divide both sides by 30:
x = 40
Therefore, 12 is 40% of 30.
Method 2: The Decimal Method
This method involves converting the percentage into a decimal and then performing a simple multiplication. The fraction 12/30 can be expressed as a decimal by dividing 12 by 30:
12 ÷ 30 = 0.4
To convert this decimal to a percentage, we multiply by 100:
0.4 x 100 = 40%
This method is particularly useful when using calculators or computer software.
Method 3: The Formula Method
A more direct formula can be used:
Percentage = (Part / Whole) x 100
In our case:
Percentage = (12 / 30) x 100 = 40%
This formula neatly summarizes the process and is highly versatile for various percentage problems.
Real-World Applications of Percentage Calculations
Understanding percentages is not just a mathematical exercise; it's a crucial skill with widespread applications in various aspects of life. Here are some examples:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. Understanding compound interest, for example, is fundamental to long-term financial planning. Calculating the percentage change in your investment portfolio is crucial for tracking performance and making informed decisions.
-
Retail and Sales: Sales discounts, markups, and profit margins are all expressed as percentages. Understanding these allows consumers to make informed purchasing decisions and businesses to effectively manage their pricing strategies. For example, a 20% off sale means you'll pay 80% of the original price.
-
Science and Statistics: Percentages are used extensively in statistical analysis to express proportions, probabilities, and error margins. Scientific research often uses percentages to present data, allowing for easier comparison and interpretation of results. For example, a clinical trial might report that 75% of patients experienced symptom relief.
-
Everyday Life: Calculating tips at restaurants, understanding nutritional information on food labels (percentage of daily value), and figuring out the percentage of completion on a project all involve percentage calculations. Even comparing prices between different stores often involves calculating percentage differences.
-
Data Analysis: In data analysis, percentages are used to represent proportions within datasets, allowing for a clearer understanding of trends and distributions. For example, a market research survey might reveal that 60% of respondents prefer a particular product.
-
Education: Grading systems in schools often rely on percentages to represent student performance. Calculating final grades, class averages, and analyzing student progress frequently involve percentage calculations.
-
Government and Politics: Government statistics, such as unemployment rates, population growth, and economic indicators, are often expressed as percentages. Understanding these statistics is crucial for civic engagement and informed decision-making.
Beyond the Basics: More Complex Percentage Problems
While the question "12 is what percent of 30?" is relatively straightforward, percentage calculations can become more complex. Consider these examples:
-
Finding the whole: If 40% of a number is 12, what is the number? This requires working backward from the percentage.
-
Finding the part: What is 25% of 80? This involves direct multiplication.
-
Percentage increase/decrease: A product's price increased from $20 to $25. What is the percentage increase? These calculations involve finding the difference and then expressing it as a percentage of the original value.
-
Percentage points: It's important to differentiate between percentage change and percentage points. For example, an increase from 10% to 15% is a 5 percentage point increase, but a 50% increase relative to the original 10%.
Mastering these more advanced applications requires a solid understanding of the fundamental principles discussed earlier.
Conclusion: The Power of Percentages
The seemingly simple question, "12 is what percent of 30?", serves as a gateway to a vast and practical world of percentage calculations. Understanding percentages is a fundamental skill applicable across various disciplines, from finance and retail to science and everyday life. By mastering different calculation methods and understanding the underlying concepts, you equip yourself with a powerful tool for navigating numerical information and making informed decisions. So, remember that 12 is 40% of 30, and utilize this knowledge to tackle more complex percentage problems with confidence.
Latest Posts
Latest Posts
-
Calculus Transcendentals 8th Edition Solutions
Sep 24, 2025
-
Gcf Of 48 And 72
Sep 24, 2025
-
Behavioral Adaptations Of A Zebra
Sep 24, 2025
-
Is Ascl5 Polar Or Nonpolar
Sep 24, 2025
-
What Times What Equals 98
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 12 Is What Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.