12 Percent As A Decimal
gasmanvison
Sep 10, 2025 · 5 min read
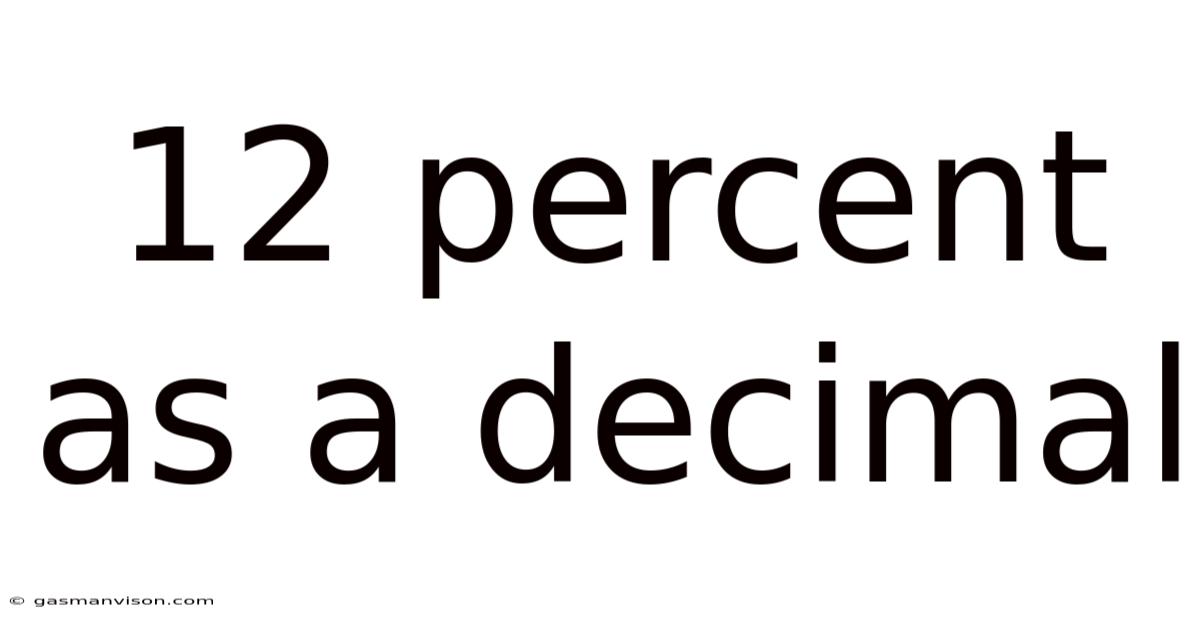
Table of Contents
12 Percent as a Decimal: A Comprehensive Guide
Meta Description: Understanding how to convert percentages to decimals is crucial for various mathematical applications. This comprehensive guide explores the conversion of 12 percent to its decimal equivalent, providing multiple methods, real-world examples, and further exploration of percentage-decimal conversions.
Percentages and decimals are fundamental concepts in mathematics and are frequently used across numerous fields, from finance and statistics to everyday calculations. Converting between these two representations is a key skill, and this article will delve into the specifics of converting 12 percent to its decimal equivalent, offering a detailed explanation and practical examples. We'll go beyond a simple answer, providing a deeper understanding of the process and its applications.
Understanding Percentages and Decimals
Before we dive into the conversion of 12 percent, let's clarify the underlying principles. A percentage represents a fraction of 100. The word "percent" itself originates from the Latin "per centum," meaning "out of one hundred." Therefore, 12 percent (12%) means 12 out of 100.
A decimal, on the other hand, is a way of representing a number using a base-10 system. It uses a decimal point to separate the whole number part from the fractional part. For example, 0.5 represents one-half (or 50%).
The relationship between percentages and decimals is direct and straightforward: a percentage can always be expressed as a decimal, and vice-versa. This interchangeability makes them powerful tools for various calculations.
Method 1: Dividing by 100
The most common and straightforward method for converting a percentage to a decimal is to divide the percentage by 100. This is because, as mentioned earlier, a percentage represents a fraction of 100.
To convert 12 percent to a decimal, we simply perform the following calculation:
12% ÷ 100 = 0.12
Therefore, 12 percent as a decimal is 0.12. This method is incredibly simple and easy to remember.
Method 2: Moving the Decimal Point
An alternative method, which is essentially a shortcut of the division method, involves moving the decimal point. Since we are dividing by 100, which is equivalent to multiplying by 1/100 or 0.01, we can simply move the decimal point two places to the left.
In the case of 12%, the implied decimal point is after the 12 (12.0%). Moving the decimal point two places to the left gives us 0.12. This approach is quicker for mental calculations, particularly with simpler percentages.
Method 3: Fraction Conversion (for a Deeper Understanding)
While the previous two methods are the most efficient, understanding the fractional representation can provide a deeper understanding of the conversion. 12% can be written as a fraction:
12/100
To convert this fraction to a decimal, we divide the numerator (12) by the denominator (100):
12 ÷ 100 = 0.12
This method reinforces the concept that a percentage is simply a fraction with a denominator of 100.
Real-World Applications of 12% as a Decimal
The decimal equivalent of 12% finds applications in numerous real-world scenarios:
-
Finance: Calculating interest rates, discounts, taxes, or profit margins often involves converting percentages to decimals. For example, a 12% interest rate on a loan translates to a 0.12 decimal multiplier used to calculate interest payments. Similarly, a 12% discount on a product would mean multiplying the product's price by 0.88 (1 - 0.12) to find the discounted price.
-
Statistics: In statistical analysis, percentages are often converted to decimals for various calculations, including probabilities and proportions. For instance, if 12% of a sample population exhibits a certain characteristic, 0.12 represents the proportion of the population with that characteristic.
-
Science: In scientific research, particularly in fields like chemistry and biology, concentration levels are often expressed as percentages which are then converted to decimals for calculations.
-
Everyday Life: From calculating tips in restaurants (e.g., a 12% tip) to determining sale prices, the conversion between percentages and decimals is a useful skill for daily calculations.
Converting Other Percentages to Decimals
The methods described above can be applied to convert any percentage to its decimal equivalent. Here are a few examples:
- 25%: 25 ÷ 100 = 0.25 (or move the decimal point two places left: 25.0% becomes 0.25)
- 5%: 5 ÷ 100 = 0.05 (or move the decimal point two places left: 5.0% becomes 0.05)
- 150%: 150 ÷ 100 = 1.5 (or move the decimal point two places left: 150.0% becomes 1.5) Note that percentages greater than 100% result in decimals greater than 1.
- 0.5%: 0.5 ÷ 100 = 0.005 (or move the decimal point two places left: 0.5% becomes 0.005)
Converting Decimals to Percentages
The reverse process is equally important. To convert a decimal to a percentage, simply multiply the decimal by 100 and add the "%" symbol.
For example:
- 0.50 becomes 50% (0.50 * 100 = 50)
- 0.02 becomes 2% (0.02 * 100 = 2)
- 1.25 becomes 125% (1.25 * 100 = 125)
Advanced Applications: Percentage Change and Growth
Understanding percentage-decimal conversions is crucial for calculating percentage change or growth. For example, if a value increases from 100 to 112, the percentage increase is calculated as follows:
(112 - 100) / 100 * 100% = 12%
In decimal terms, this 12% increase can be represented as 0.12. This is often used in financial analysis, where tracking percentage growth in investments or sales is essential.
Conclusion
Converting 12 percent to its decimal equivalent (0.12) is a straightforward process with multiple approaches. Mastering this conversion is vital for various mathematical applications across diverse fields. Whether using division, decimal point movement, or fractional conversion, understanding the underlying principles ensures accurate calculations and a deeper understanding of percentages and decimals, making them invaluable tools in everyday life and professional settings. Remember to practice regularly to solidify your understanding and improve your proficiency in these essential mathematical concepts. The ability to seamlessly convert between percentages and decimals is a skill that will serve you well in numerous contexts.
Latest Posts
Latest Posts
-
Which Statements Characterize Serous Membranes
Sep 10, 2025
-
What Is 20 Of 85
Sep 10, 2025
-
15 18 In Lowest Terms
Sep 10, 2025
-
What Times What Equals 26
Sep 10, 2025
-
An Eap Is An Automotive
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 12 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.