17/12 As A Mixed Number
gasmanvison
Sep 09, 2025 · 5 min read
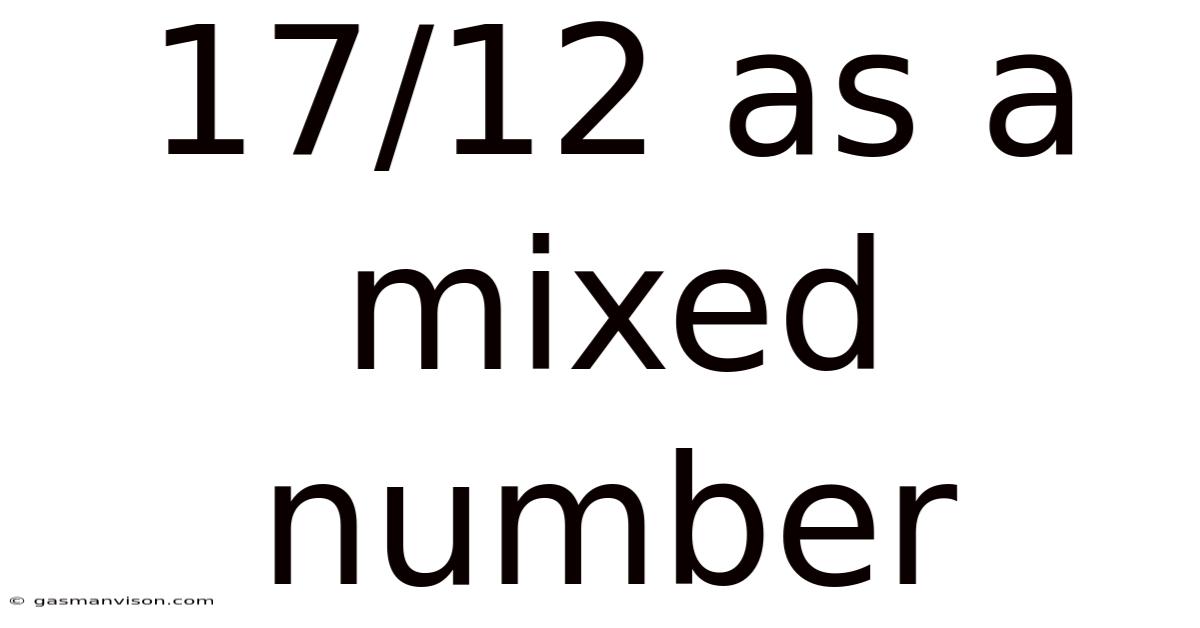
Table of Contents
Understanding 17/12 as a Mixed Number: A Comprehensive Guide
Meta Description: Learn how to convert the improper fraction 17/12 into a mixed number. This comprehensive guide explains the process step-by-step, covering the definition of mixed numbers, practical examples, and troubleshooting common mistakes. We'll explore the concept thoroughly, making it easy for everyone to grasp.
Converting fractions is a fundamental skill in mathematics, crucial for various applications from baking to advanced calculus. One common task involves transforming improper fractions (where the numerator is larger than the denominator) into mixed numbers. This guide focuses specifically on converting the improper fraction 17/12 into a mixed number, explaining the process thoroughly and addressing potential areas of confusion. We’ll delve into the underlying principles, providing a solid understanding for anyone tackling this type of problem.
What is a Mixed Number?
Before diving into the conversion, let's clarify what a mixed number is. A mixed number combines a whole number and a proper fraction (where the numerator is smaller than the denominator). For instance, 1 ½ is a mixed number; it represents one whole unit and one-half of another. Understanding this definition is key to comprehending the conversion process from improper fractions.
Converting 17/12 to a Mixed Number: A Step-by-Step Approach
The improper fraction 17/12 indicates that we have 17 parts, each representing one-twelfth of a whole. To convert this into a mixed number, we need to determine how many whole units are contained within 17/12 and what fraction remains.
Step 1: Division
The core of the conversion lies in dividing the numerator (17) by the denominator (12). Performing the division, we get:
17 ÷ 12 = 1 with a remainder of 5
Step 2: Interpreting the Result
The quotient (1) represents the whole number part of our mixed number. The remainder (5) becomes the numerator of the fractional part, while the denominator remains the same (12).
Step 3: Constructing the Mixed Number
Combining the whole number and the fraction, we arrive at the mixed number representation of 17/12:
17/12 = 1 5/12
Why Use Mixed Numbers?
While both improper fractions and mixed numbers represent the same quantity, mixed numbers often offer better readability and understanding in practical contexts. Imagine a recipe calling for 17/12 cups of flour. Saying "one and five-twelfths cups" is considerably clearer and easier to visualize than "seventeen-twelfths cups." This improved clarity makes mixed numbers particularly useful in everyday applications and real-world problem-solving.
Further Examples: Reinforcing the Concept
Let's solidify our understanding with a few more examples of converting improper fractions to mixed numbers. This will highlight the versatility and consistency of the method:
-
22/5: 22 ÷ 5 = 4 with a remainder of 2. Therefore, 22/5 = 4 2/5
-
31/8: 31 ÷ 8 = 3 with a remainder of 7. Therefore, 31/8 = 3 7/8
-
19/6: 19 ÷ 6 = 3 with a remainder of 1. Therefore, 19/6 = 3 1/6
These examples demonstrate the consistent application of the division method. The quotient becomes the whole number, and the remainder forms the numerator of the fraction, maintaining the original denominator.
Common Mistakes and How to Avoid Them
Even with a seemingly straightforward process, some common mistakes can occur during the conversion. Let's address them:
-
Incorrect Division: Ensure you accurately perform the division of the numerator by the denominator. A minor error in division will result in an incorrect mixed number. Double-check your calculations to prevent this.
-
Misinterpreting Remainder: Pay close attention to the remainder. It's the crucial element forming the numerator of the fractional part in the mixed number. Failing to use the remainder correctly leads to an inaccurate result.
-
Forgetting the Denominator: Remember that the denominator of the fraction in the mixed number remains unchanged from the original improper fraction. This is a common oversight leading to errors.
By carefully following the steps and double-checking calculations, these mistakes can be easily avoided.
Simplifying Mixed Numbers: A Further Step
Sometimes, the fractional part of the mixed number can be simplified. Let's revisit our original example, 1 5/12. In this instance, the fraction 5/12 cannot be simplified further because 5 and 12 share no common factors other than 1. However, consider the mixed number 4 6/12. Here, the fraction 6/12 can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 6. This simplifies to ½. Therefore, 4 6/12 simplifies to 4 ½. Always check for simplification opportunities to present the mixed number in its most concise form.
Applications of Mixed Numbers in Real Life
Mixed numbers are frequently encountered in various aspects of daily life, including:
-
Cooking and Baking: Recipes often use mixed numbers to specify ingredient quantities (e.g., 2 ½ cups of flour).
-
Measurement: Measuring lengths, weights, and volumes frequently involves mixed numbers (e.g., 3 ¼ inches).
-
Time: Telling time involves understanding mixed numbers (e.g., 1:45 or 1 ¾ hours).
Mastering the conversion from improper fractions to mixed numbers empowers you to navigate these scenarios with confidence and precision.
Converting Mixed Numbers back to Improper Fractions
It's also important to understand the reverse process: converting a mixed number back into an improper fraction. This involves multiplying the whole number by the denominator, adding the numerator, and placing the result over the original denominator. For example, to convert 1 5/12 back to an improper fraction:
(1 * 12) + 5 = 17
The improper fraction is therefore 17/12. This reciprocal understanding strengthens your grasp of fractional manipulation.
Conclusion: Mastering the Conversion
Converting the improper fraction 17/12 to the mixed number 1 5/12 is a straightforward process once you understand the fundamental steps of division, interpretation, and construction. By mastering this skill, you equip yourself with a valuable tool for various mathematical applications and real-world problem-solving. Remember to always double-check your calculations and look for opportunities to simplify the resulting mixed number. With consistent practice and attention to detail, you'll confidently navigate the world of fractions and mixed numbers.
Latest Posts
Latest Posts
-
5n 34 2 1 7n
Sep 10, 2025
-
Which Reaction Represents Cellular Respiration
Sep 10, 2025
-
3 Oz Is How Much
Sep 10, 2025
-
Convert 9 7 Liters To Milliliters
Sep 10, 2025
-
Choose The Correctly Punctuated Sentences
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 17/12 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.