2 X 7 3x 12
gasmanvison
Sep 16, 2025 · 5 min read
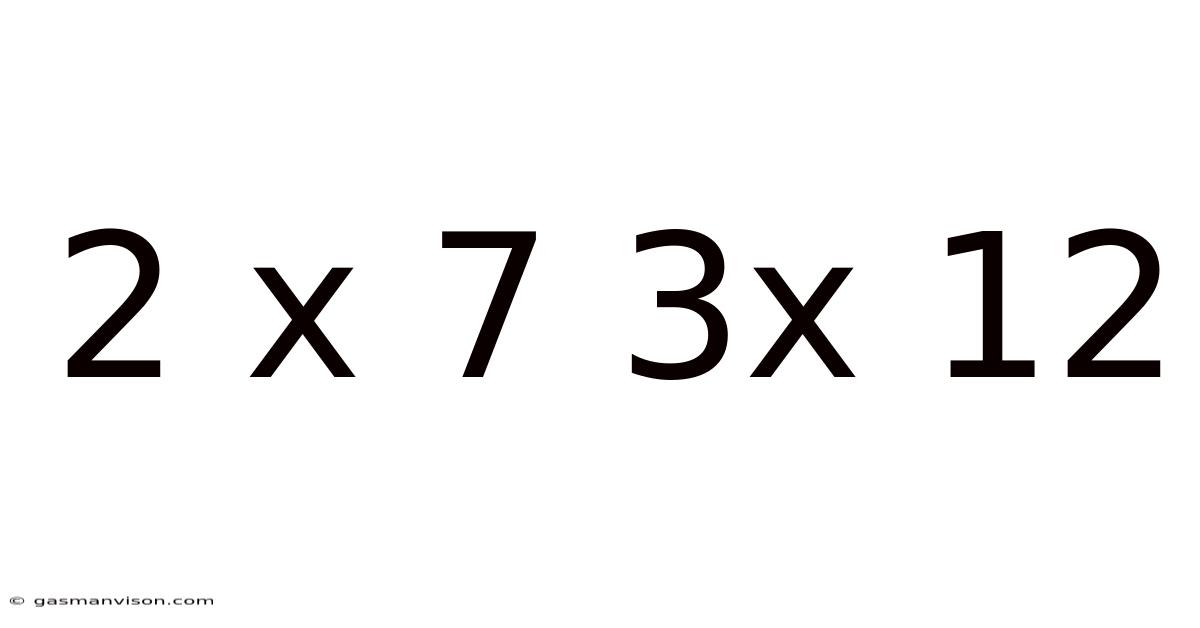
Table of Contents
Decoding the Enigma: Exploring the Mathematical Relationship Between 2x7 and 3x12
This article delves into the seemingly simple yet surprisingly rich mathematical relationship between the expressions 2 x 7 and 3 x 12. While at first glance they appear as unrelated multiplication problems, a closer examination reveals fascinating connections involving prime factorization, least common multiples, greatest common divisors, and their broader implications in algebra and number theory. This exploration will go beyond simple calculation, revealing the underlying structure and patterns that govern these seemingly basic mathematical operations.
Understanding the Fundamentals: Prime Factorization and the Building Blocks of Numbers
Before diving into the comparison of 2 x 7 and 3 x 12, let's establish a foundational understanding of prime factorization. Prime factorization is the process of expressing a number as a product of its prime numbers. Prime numbers are whole numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.). This decomposition is unique for every number and forms the bedrock of many advanced mathematical concepts.
Let's factorize the results of our expressions:
-
2 x 7 = 14: The prime factorization of 14 is 2 x 7. This indicates that 14 is composed of one factor of 2 and one factor of 7.
-
3 x 12 = 36: The prime factorization of 36 is 2 x 2 x 3 x 3, or 2² x 3². This shows that 36 is composed of two factors of 2 and two factors of 3.
The prime factorization reveals a key difference: 14 has distinct prime factors (2 and 7), while 36 is composed of repeated prime factors (2 and 3). This seemingly small distinction has significant implications when exploring concepts like least common multiples (LCM) and greatest common divisors (GCD).
Exploring Relationships: Least Common Multiple (LCM) and Greatest Common Divisor (GCD)
The LCM and GCD are crucial concepts in number theory that describe the relationship between two or more numbers.
-
Least Common Multiple (LCM): The LCM is the smallest positive integer that is divisible by all the given numbers. It represents the smallest number that contains all the prime factors of the involved numbers, with each prime factor appearing at least as many times as it appears in any of the individual numbers.
-
Greatest Common Divisor (GCD): The GCD is the largest positive integer that divides all the given numbers without leaving a remainder. It represents the largest number that is a factor of all the involved numbers.
Let's calculate the LCM and GCD of 14 and 36:
Finding the LCM of 14 and 36:
- Prime Factorization: 14 = 2 x 7; 36 = 2² x 3²
- Identify Highest Powers: The highest power of 2 is 2², the highest power of 3 is 3², and the highest power of 7 is 7¹.
- Multiply: LCM(14, 36) = 2² x 3² x 7 = 4 x 9 x 7 = 252
Finding the GCD of 14 and 36:
- Prime Factorization: 14 = 2 x 7; 36 = 2² x 3²
- Identify Common Factors: The only common prime factor is 2, and its lowest power is 2¹.
- Multiply: GCD(14, 36) = 2 = 2
The LCM and GCD highlight the differences in the composition of 14 and 36. The LCM (252) represents the smallest number divisible by both, while the GCD (2) reveals that 2 is the only common factor they share.
Extending the Analysis: Applications in Algebra and Number Theory
The seemingly simple calculations of 2 x 7 and 3 x 12 have far-reaching implications in more advanced mathematical fields:
-
Diophantine Equations: These equations involve finding integer solutions. The LCM and GCD are crucial tools in solving certain types of Diophantine equations. For instance, understanding the relationship between 14 and 36 helps in determining potential solutions for equations where 14 and 36 are coefficients or constants.
-
Modular Arithmetic: This branch of number theory deals with remainders after division. The LCM and GCD play essential roles in understanding cyclical patterns and solving congruences. The properties of 14 and 36, particularly their LCM, would influence the behavior of numbers within specific modulo systems.
-
Abstract Algebra: Concepts like groups, rings, and fields, fundamental to abstract algebra, rely heavily on the properties of numbers and their relationships, as highlighted by the prime factorization, LCM, and GCD analyses of 14 and 36.
-
Cryptography: The prime factorization of numbers is the cornerstone of many modern encryption algorithms. Understanding the difficulty in factoring large numbers into their prime components forms the basis of secure communication systems. While 14 and 36 are relatively small, the principles involved extend to much larger numbers used in cryptography.
Beyond Calculation: The Significance of Mathematical Exploration
The exploration of the relationship between 2 x 7 and 3 x 12 transcends simple arithmetic. It demonstrates the power of breaking down complex concepts into their fundamental building blocks. The seemingly trivial exercise of multiplying two numbers reveals a deeper mathematical structure that extends to advanced areas like number theory, algebra, and even cryptography.
This analysis highlights the importance of:
-
Fundamental Concepts: Mastering basic mathematical operations like multiplication and prime factorization is crucial for tackling more advanced topics.
-
Pattern Recognition: Identifying patterns and relationships between numbers allows for a deeper understanding of mathematical structures.
-
Analytical Thinking: Breaking down problems into smaller, manageable components facilitates the discovery of hidden relationships and solutions.
-
Connecting Concepts: Understanding the connections between seemingly disparate areas of mathematics strengthens overall mathematical understanding and problem-solving abilities.
Conclusion: A Deeper Dive into the Seemingly Simple
The seemingly straightforward comparison of 2 x 7 and 3 x 12 opens a window into the fascinating world of number theory and its diverse applications. By analyzing prime factorization, LCM, GCD, and their implications in various mathematical fields, we uncover a richness and depth far exceeding the initial simplicity of the problem. This exercise emphasizes the importance of exploring mathematical concepts beyond superficial calculations, fostering a deeper appreciation for the underlying structure and elegance of mathematics. It encourages a mindset of inquiry and discovery, inviting further exploration of mathematical relationships and patterns that lie hidden within seemingly simple numerical expressions. The journey from 2 x 7 to 3 x 12 is not merely a calculation but a gateway to a broader understanding of the beauty and power of mathematics.
Latest Posts
Latest Posts
-
Three Components Of A Nucleotide
Sep 16, 2025
-
6 Cups To Fl Oz
Sep 16, 2025
-
What Times What Equals 52
Sep 16, 2025
-
What Is The Brightest Color
Sep 16, 2025
-
Simplify Square Root Of 63
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 2 X 7 3x 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.