3 3/4 X 2 4/5
gasmanvison
Sep 07, 2025 · 5 min read
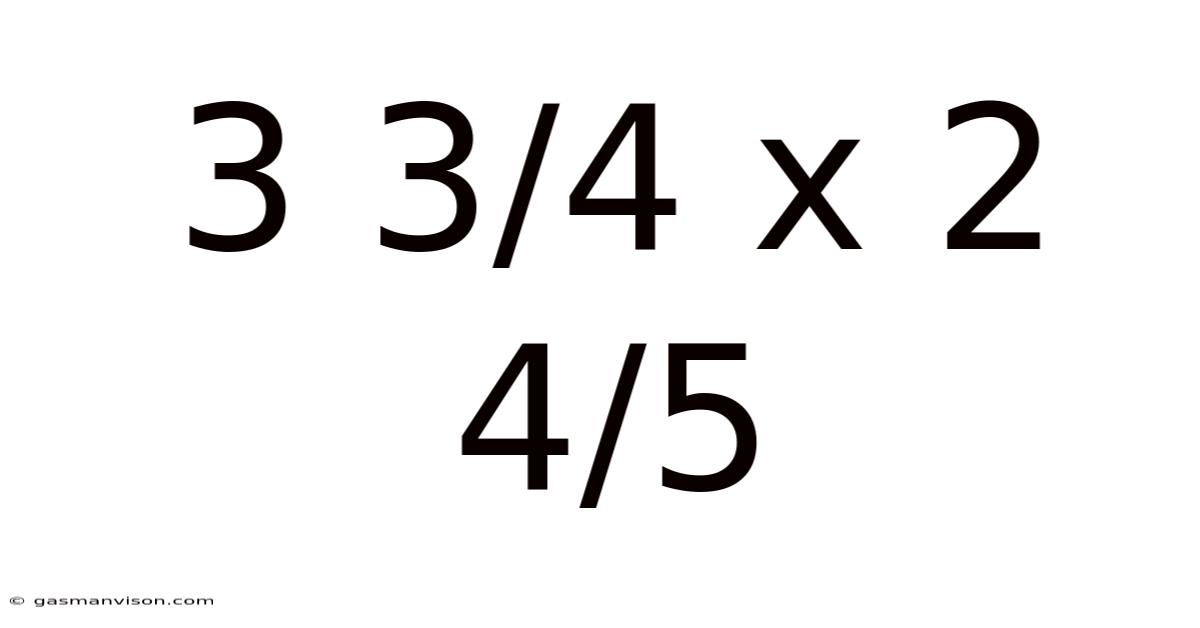
Table of Contents
Decoding 3 3/4 x 2 4/5: A Deep Dive into Mixed Number Multiplication
This article explores the seemingly simple problem of multiplying mixed numbers, specifically 3 3/4 x 2 4/5. While the calculation itself might appear straightforward, understanding the underlying principles and exploring different solution methods offers valuable insights into fundamental mathematical concepts and their applications. This detailed explanation caters to various learning styles, providing both a step-by-step guide and a broader contextual understanding of mixed number multiplication. We'll also delve into the practical applications of this seemingly simple calculation and discuss its relevance in various fields.
Understanding Mixed Numbers
Before tackling the multiplication, let's solidify our understanding of mixed numbers. A mixed number combines a whole number and a fraction. For example, 3 3/4 represents three whole units and three-quarters of another unit. Understanding this representation is crucial for performing calculations efficiently. The key is to recognize that a mixed number is simply a different way of expressing an improper fraction (a fraction where the numerator is larger than the denominator).
Converting Mixed Numbers to Improper Fractions: The Crucial First Step
The most efficient way to multiply mixed numbers is to first convert them into improper fractions. This simplifies the multiplication process significantly. To convert a mixed number to an improper fraction, follow these steps:
- Multiply the whole number by the denominator: For 3 3/4, we multiply 3 (the whole number) by 4 (the denominator) which equals 12.
- Add the numerator: Add the result from step 1 (12) to the numerator (3). This gives us 15.
- Keep the denominator: The denominator remains the same (4).
Therefore, 3 3/4 is equivalent to the improper fraction 15/4.
Following the same procedure for 2 4/5:
- Multiply 2 (whole number) by 5 (denominator): 2 x 5 = 10
- Add the numerator: 10 + 4 = 14
- Keep the denominator: The denominator remains 5.
So, 2 4/5 is equivalent to 14/5.
Multiplying Improper Fractions: A Straightforward Process
Now that we have converted our mixed numbers into improper fractions (15/4 and 14/5), multiplying them becomes a straightforward process:
- Multiply the numerators: 15 x 14 = 210
- Multiply the denominators: 4 x 5 = 20
This gives us the improper fraction 210/20.
Simplifying the Result: Converting Back to a Mixed Number
The improper fraction 210/20 represents our answer, but it's generally preferred to express the answer as a mixed number or a simplified fraction. To simplify 210/20, we find the greatest common divisor (GCD) of 210 and 20, which is 10. Dividing both the numerator and the denominator by 10, we get:
210 ÷ 10 = 21 20 ÷ 10 = 2
This simplifies our fraction to 21/2.
Converting the Improper Fraction to a Mixed Number
Finally, let's convert the improper fraction 21/2 to a mixed number:
- Divide the numerator by the denominator: 21 ÷ 2 = 10 with a remainder of 1.
- The quotient becomes the whole number: The quotient (10) becomes the whole number part of our mixed number.
- The remainder becomes the numerator: The remainder (1) becomes the numerator of the fraction part.
- The denominator remains the same: The denominator remains 2.
Therefore, 21/2 is equal to 10 1/2.
Therefore, 3 3/4 x 2 4/5 = 10 1/2
Alternative Methods for Multiplication
While the method above is the most efficient for most cases, alternative methods exist, particularly useful for visualizing the process. These include:
-
Distributive Property: This method involves expanding the mixed numbers and then applying the distributive property of multiplication over addition. While possible, it's generally more complex than the improper fraction method.
-
Visual Representation: Using diagrams or area models can be helpful, especially for visual learners. This involves representing the mixed numbers as areas and finding the product through visualization. However, for larger numbers, this method can become cumbersome.
Real-World Applications of Mixed Number Multiplication
The seemingly simple calculation of 3 3/4 x 2 4/5 has far-reaching applications in various fields:
-
Baking and Cooking: Recipes often require precise measurements involving fractions and mixed numbers. Calculating the amount of ingredients needed for a larger batch involves multiplying mixed numbers.
-
Construction and Engineering: Precise measurements are crucial in construction and engineering. Calculating dimensions, material quantities, and distances often involves mixed number multiplication.
-
Sewing and Tailoring: Pattern making and fabric cutting require accurate measurements involving fractions and mixed numbers. Calculating the amount of fabric needed for a project involves multiplying mixed numbers.
-
Financial Calculations: Calculating interest, discounts, or profit margins may sometimes involve mixed numbers.
-
Data Analysis: In statistical analysis, dealing with averages and proportions might involve mixed numbers.
Advanced Concepts and Extensions
This seemingly basic calculation opens doors to more advanced mathematical concepts:
-
Understanding different number systems: The exercise emphasizes the importance of number representation and the ease of computation with different forms (mixed numbers versus improper fractions).
-
Order of operations: Understanding the order of operations becomes crucial when dealing with more complex expressions involving mixed numbers and other arithmetic operations.
-
Algebraic applications: The concepts are easily extendable to algebraic expressions involving variables and mixed numbers.
-
Decimal equivalents: Converting mixed numbers to decimals and then performing multiplication is another viable approach, especially with the aid of calculators.
Conclusion:
The multiplication of 3 3/4 x 2 4/5, although seemingly simple, provides a rich learning opportunity. It reinforces fundamental mathematical concepts, illustrates the importance of efficient calculation methods, and highlights the practical applications of these concepts in various real-world scenarios. Mastering this seemingly basic calculation forms a solid foundation for tackling more complex mathematical problems in the future. The exploration of alternative methods and the connection to broader mathematical principles enhances the understanding and appreciation of this fundamental arithmetic operation. The focus on improper fractions and their subsequent simplification reinforces a deeper understanding of fraction manipulation and is crucial for successful problem-solving in more complex mathematical contexts.
Latest Posts
Latest Posts
-
Ca3 Po4 2 Compound Name
Sep 08, 2025
-
Area Of 6 Inch Circle
Sep 08, 2025
-
Legal Drinking Age Date Today
Sep 08, 2025
-
What Is 40 Of 120
Sep 08, 2025
-
5 Square Root Of 3
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about 3 3/4 X 2 4/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.