3 Less Than A Number
gasmanvison
Sep 10, 2025 · 6 min read
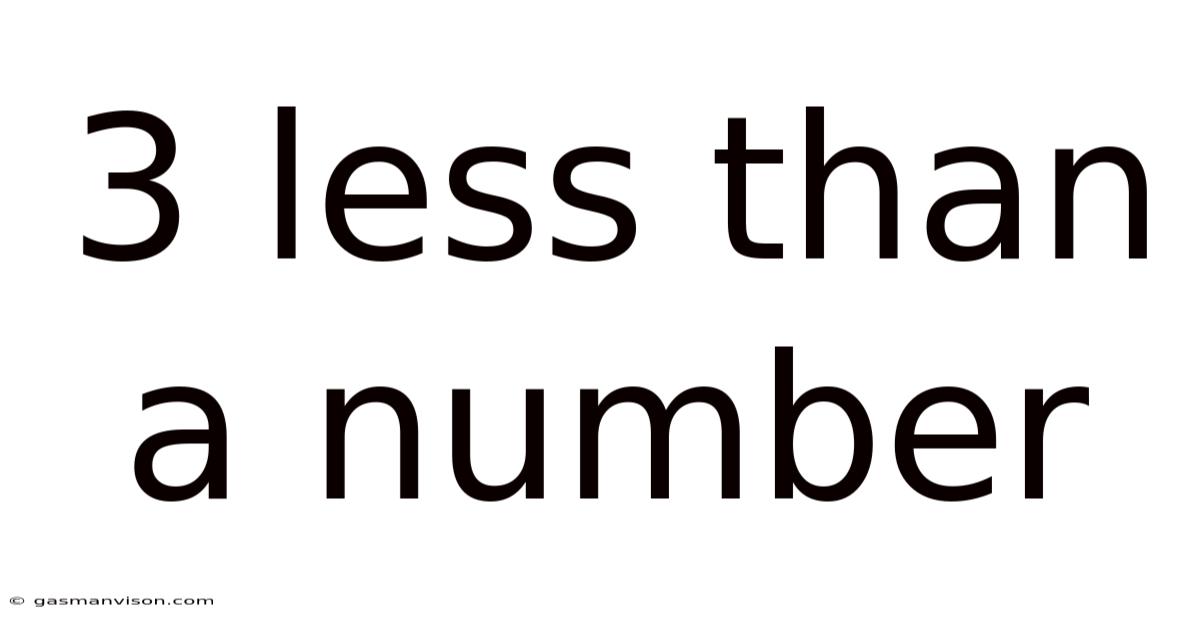
Table of Contents
3 Less Than a Number: Exploring Mathematical Concepts and Real-World Applications
This article delves into the seemingly simple phrase "3 less than a number," exploring its mathematical representation, diverse applications, and the broader concepts it touches upon. While seemingly basic, this expression serves as a foundational building block for understanding more complex algebraic equations and problem-solving techniques. We will explore its use in various contexts, from simple arithmetic to more advanced mathematical fields. This comprehensive guide will also cover related concepts like inequalities, variables, and the significance of precise mathematical language.
Meta Description: Uncover the mathematical meaning and applications of "3 less than a number." This detailed guide explores its use in arithmetic, algebra, real-world problems, and advanced mathematical concepts. Learn how to represent it mathematically and solve related problems efficiently.
Understanding the Expression: "3 Less Than a Number"
The phrase "3 less than a number" implies a subtraction operation. It signifies that we are taking 3 away from an unknown quantity, which we represent as a variable. In mathematics, we typically use letters like x, y, or n to represent these unknown quantities. Therefore, "3 less than a number" translates mathematically to: n - 3 or x - 3 or any other suitable variable minus 3. The key takeaway is that the "3" is subtracted from the number, not the other way around. This seemingly small detail is crucial for accurate mathematical representation and problem-solving.
This seemingly simple expression forms the basis of many algebraic equations. Understanding its structure and representation is crucial for building a strong foundation in algebra and related fields. The simplicity of this expression allows for easy comprehension, making it an ideal starting point for introducing algebraic concepts to beginners. Later, we'll see how easily this basic understanding scales to more complex scenarios.
Representing "3 Less Than a Number" in Equations
Let's explore how this phrase appears in various equation types. Understanding how to translate word problems into mathematical equations is a key skill in algebra and problem-solving.
-
Simple Equations: Consider the problem: "3 less than a number is 10." This translates directly to the equation:
x - 3 = 10. Solving this equation involves adding 3 to both sides, yieldingx = 13. Therefore, the number is 13. This illustrates the straightforward application of the expression in forming and solving basic algebraic equations. -
Inequalities: The concept extends to inequalities as well. For instance, "3 less than a number is greater than 5" can be written as:
x - 3 > 5. Solving this inequality involves adding 3 to both sides, resulting inx > 8. This shows that the number must be greater than 8. This expands the application of the core expression to situations involving ranges of values rather than single solutions. -
Compound Inequalities: The expression can also be incorporated into more complex inequalities. "3 less than a number is between 2 and 8" translates to:
2 < x - 3 < 8. Solving this requires adding 3 to all parts of the inequality, giving5 < x < 11. This showcases the adaptability of the expression within more intricate mathematical structures. Mastering these compound inequalities is essential for tackling more challenging problems. -
Word Problems: Many word problems require translating the phrase "3 less than a number" into a mathematical representation before solving. For example: "John has a certain number of apples. If he gives away 3 apples, he has 7 left. How many apples did he start with?" This problem can be expressed as:
x - 3 = 7, with 'x' representing the initial number of apples. Solving this givesx = 10, indicating John started with 10 apples. This practical application highlights the real-world relevance of this seemingly simple mathematical concept.
Advanced Applications and Related Concepts
While the basic application is straightforward, the concept of "3 less than a number" touches upon several more advanced mathematical concepts.
-
Functions: The expression can be used to define a function. For example, f(x) = x - 3 represents a linear function where the output (f(x)) is always 3 less than the input (x). This introduces the concept of input-output relationships and lays the groundwork for understanding more complex functional relationships. Understanding function notation is crucial for progressing in mathematics and related fields like computer science.
-
Sequences and Series: The concept can be integrated into defining sequences. Consider a sequence where each term is 3 less than the previous term. This type of sequence can be represented using recursive formulas and demonstrates a practical application of subtraction within sequential patterns. This provides insight into number patterns and their mathematical representation.
-
Calculus: While not directly evident, the underlying concept of subtraction and its relationship to change are fundamental to the study of calculus. The concept of a derivative, for instance, involves finding the instantaneous rate of change, which fundamentally depends on understanding differences (or changes) in values. This provides a glimpse into how seemingly basic mathematical concepts form the cornerstone of more advanced mathematical studies.
-
Abstract Algebra: In abstract algebra, the concept of subtraction can be generalized to other mathematical structures. While this is beyond the scope of a basic introduction, it illustrates that even simple concepts like "3 less than a number" have deep connections to advanced mathematical fields.
Real-World Applications
The simplicity of "3 less than a number" belies its widespread applicability in various real-world scenarios:
-
Age Problems: "Sarah is 3 years younger than her brother." If we let 'x' represent the brother's age, Sarah's age can be represented as
x - 3. This showcases how the expression simplifies the modeling of age relationships. -
Financial Calculations: "A product costs $3 less than its original price." Representing the original price as 'x', the current price can be expressed as
x - 3. This demonstrates its relevance in financial calculations and pricing strategies. -
Measurement Conversions: Consider converting temperatures from Celsius to Fahrenheit. While the conversion formula is more complex, the core concept of subtracting a constant value is integral to the process.
-
Inventory Management: If a store sells 3 units of a certain product, the remaining stock can be represented as
x - 3, where 'x' is the initial stock level. -
Physics and Engineering: Various physical phenomena involve subtracting constant values. These applications often involve understanding changes or differences in physical quantities.
Importance of Precise Mathematical Language
The accurate use of mathematical language is crucial for clear communication and avoiding misunderstandings. For example, "3 less than a number" is distinctly different from "a number less than 3." The former represents x - 3, while the latter represents x < 3. This subtle difference highlights the importance of paying close attention to the order of operations and the precise wording used in mathematical expressions.
Conclusion
The expression "3 less than a number," although seemingly simple, provides a foundational understanding of algebraic concepts, inequalities, and their real-world applications. Its use extends far beyond simple arithmetic problems, touching upon advanced mathematical fields and providing a vital building block for more complex calculations. Mastering this seemingly simple concept and understanding its broader implications is crucial for anyone aiming to build a strong foundation in mathematics and its related fields. By thoroughly understanding this concept, you build a firm base for tackling increasingly complex mathematical problems. The seemingly simple act of subtracting 3 from a number unlocks a gateway to a world of mathematical possibilities.
Latest Posts
Latest Posts
-
5 2 Independent Practice Answer Key
Sep 10, 2025
-
C3h5 No3 3 Molar Mass
Sep 10, 2025
-
Staph Infection Cholera E Coli
Sep 10, 2025
-
What Does Cpu Stand For
Sep 10, 2025
-
As Electrons Move They Make
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 3 Less Than A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.