3 Times What Equals 2
gasmanvison
Sep 09, 2025 · 5 min read
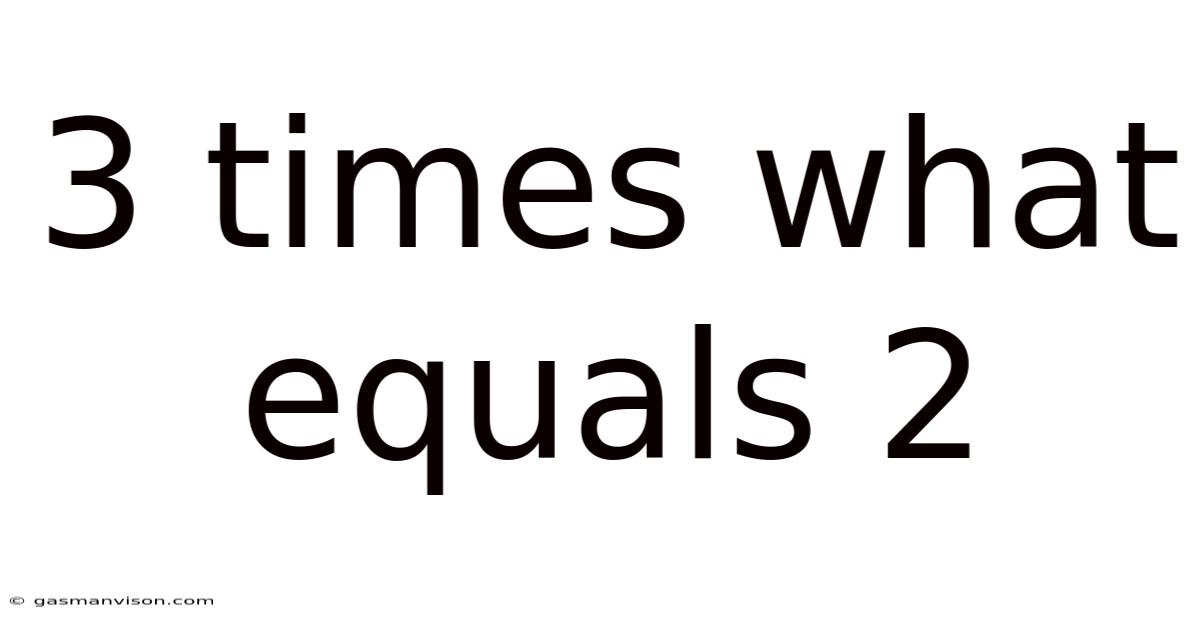
Table of Contents
3 Times What Equals 2: Unraveling the Mystery of Fractional Equations
This seemingly simple question, "3 times what equals 2," hides a surprising depth of mathematical concepts. While the immediate answer might seem elusive to some, understanding its solution opens doors to comprehending fundamental algebraic principles, their applications in real-world scenarios, and even the fascinating world of abstract mathematics. This article will delve into various methods of solving this equation, explore its practical implications, and touch upon related mathematical ideas. It will also address common misconceptions and provide a robust understanding of the underlying principles.
Understanding the Problem: A Foundation in Algebra
The core of the problem, "3 times what equals 2," can be expressed algebraically as the equation 3x = 2, where 'x' represents the unknown value we're trying to find. This is a simple linear equation, one of the most fundamental types of equations in algebra. Solving for 'x' involves isolating it on one side of the equation through a series of carefully applied mathematical operations.
Method 1: The Division Approach – A Direct Solution
The most straightforward way to solve 3x = 2 is by dividing both sides of the equation by 3. This maintains the equality while isolating 'x'.
- Step 1: 3x = 2
- Step 2: Divide both sides by 3: (3x)/3 = 2/3
- Step 3: Simplify: x = 2/3
Therefore, the answer is 2/3. Three times two-thirds equals two. This simple division method highlights the core principle of maintaining balance in an equation. Any operation performed on one side must be mirrored on the other to preserve the equality.
Method 2: The Reciprocal Approach – Leveraging Multiplicative Inverses
Another approach uses the concept of reciprocals or multiplicative inverses. The reciprocal of a number is the number that, when multiplied by the original number, results in 1. The reciprocal of 3 is 1/3.
- Step 1: 3x = 2
- Step 2: Multiply both sides by the reciprocal of 3 (which is 1/3): (1/3) * 3x = (1/3) * 2
- Step 3: Simplify: x = 2/3
This method reinforces the idea that multiplication and division are inverse operations; they undo each other. Using reciprocals offers a slightly different perspective on solving the equation, solidifying the understanding of inverse operations.
Method 3: Visual Representation – Understanding Fractions Geometrically
For a more intuitive grasp, consider a visual representation. Imagine a whole divided into three equal parts. The question "3 times what equals 2" can be visualized as finding two of those three parts. Each part represents 1/3, and two parts together represent 2/3. This visual approach bridges the gap between abstract algebraic concepts and concrete representations, aiding comprehension for visual learners.
Real-World Applications: Beyond the Textbook
While this might seem like a purely abstract mathematical problem, the concept of solving equations like 3x = 2 has far-reaching applications in various real-world scenarios:
-
Recipe Scaling: Imagine you have a recipe that calls for 3 cups of flour and yields 2 cakes. To find out how much flour is needed for one cake, you'd solve the equation 3x = 2, with 'x' representing the flour needed per cake. The answer, 2/3 cup, is crucial for accurate scaling.
-
Unit Conversion: Converting units frequently involves solving similar equations. For example, if 3 meters of fabric costs $2, finding the cost per meter would involve solving 3x = 2, where 'x' represents the cost per meter.
-
Rate Problems: Many rate problems in physics, engineering, and everyday life can be modeled using linear equations. For instance, if a machine produces 3 widgets in 2 hours, solving 3x = 2 helps determine the rate of production (widgets per hour).
-
Proportional Reasoning: This equation is a classic example of a proportion. Understanding proportions is fundamental in various fields, including finance, statistics, and engineering. Scaling maps, designing models, and calculating concentrations all rely heavily on proportional reasoning.
-
Financial Calculations: Simple interest calculations, determining profit margins, or calculating unit costs all utilize similar algebraic principles. Understanding these fundamental equations is critical for sound financial decision-making.
Extending the Concept: More Complex Equations
The seemingly simple equation 3x = 2 serves as a stepping stone to more complex algebraic problems. Understanding its solution provides a solid foundation for tackling more challenging equations, including:
-
Equations with Multiple Variables: Equations involving more than one variable often require solving for one variable in terms of the others. The techniques used to solve 3x = 2 are essential building blocks for these more complex scenarios.
-
Systems of Equations: Many real-world problems require solving multiple equations simultaneously. The ability to solve simple linear equations is paramount to tackling systems of equations using methods like substitution or elimination.
-
Quadratic Equations: While more advanced, quadratic equations (equations involving x²) share some fundamental similarities with linear equations. The principles learned from solving simple linear equations like 3x = 2 are helpful in understanding and approaching quadratic equations.
-
Higher-Order Equations: The methods and concepts used to solve linear equations are foundational to understanding higher-order equations (equations with powers of x greater than 1).
Addressing Common Misconceptions
Many students struggle with fractional answers. The answer 2/3 might seem unusual compared to whole number solutions. However, it's crucial to understand that fractions are perfectly valid and often necessary solutions to mathematical problems, particularly in real-world applications where exact values are crucial.
Conclusion: A Foundation for Mathematical Understanding
The deceptively simple equation, 3 times what equals 2, offers a gateway to a vast world of mathematical concepts. Solving this equation not only provides the answer (2/3) but also strengthens the understanding of fundamental algebraic principles, including:
-
The concept of inverse operations: Understanding how multiplication and division undo each other is critical for solving various algebraic equations.
-
Maintaining equality in equations: Performing the same operation on both sides of an equation is fundamental for solving equations while preserving their validity.
-
Working with fractions: Fractions are an integral part of mathematics, and solving this equation highlights their importance in expressing solutions.
-
Applying mathematical concepts to real-world problems: The applications of solving this equation extend to various fields, demonstrating the practical relevance of mathematics.
By mastering the solution to this seemingly simple problem, learners build a strong foundation for tackling more complex mathematical challenges and appreciating the power and elegance of algebra in solving real-world problems. It’s a small equation with a big impact on mathematical understanding.
Latest Posts
Latest Posts
-
X 8 23 4 36
Sep 11, 2025
-
How Many Inches Is 27cm
Sep 11, 2025
-
How Did Linnaean Classify Organisms
Sep 11, 2025
-
What Is 75 Of 150
Sep 11, 2025
-
Which Statement Best Describes Wellness
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 3 Times What Equals 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.