7 1/2 Divided By 3/4
gasmanvison
Sep 04, 2025 · 5 min read
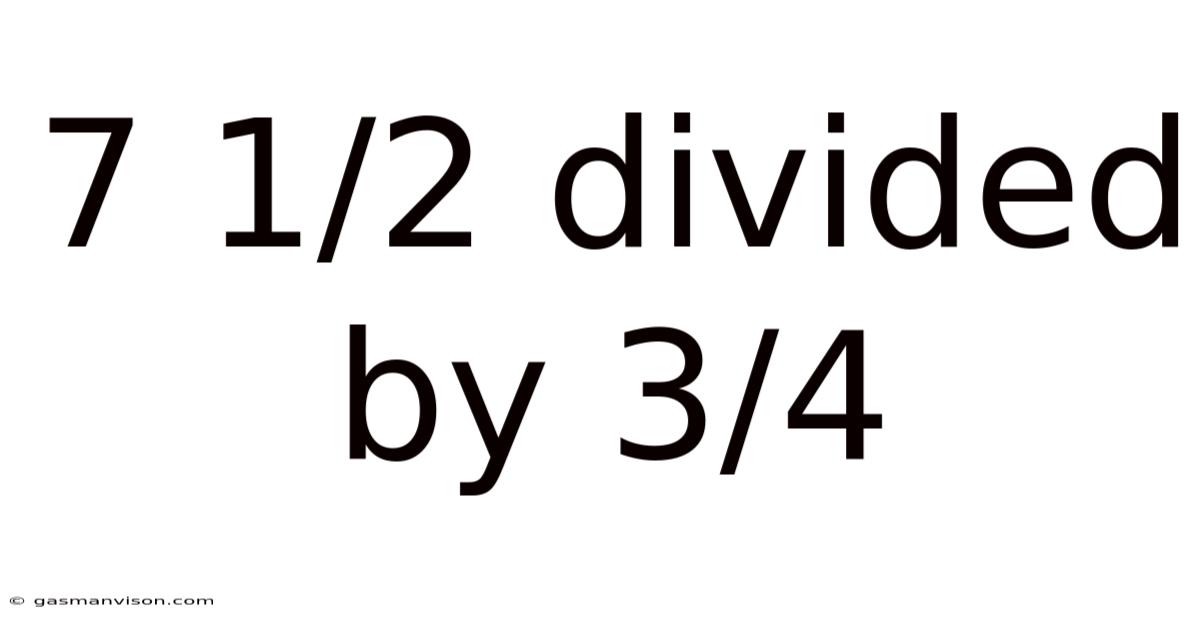
Table of Contents
Decoding 7 1/2 Divided by 3/4: A Comprehensive Guide to Fraction Division
Meta Description: Learn how to solve 7 1/2 divided by 3/4 step-by-step. This comprehensive guide breaks down the process of dividing mixed numbers, offering multiple methods and practical examples for a complete understanding of fraction division. Master this fundamental math concept with ease!
Dividing fractions, especially mixed numbers like 7 1/2 divided by 3/4, can seem daunting at first. However, with a systematic approach and a clear understanding of the underlying principles, this seemingly complex calculation becomes surprisingly straightforward. This guide will not only show you how to solve 7 1/2 ÷ 3/4 but also equip you with the knowledge and strategies to tackle similar fraction division problems confidently. We'll explore multiple methods, explaining each step thoroughly, and providing ample opportunities to reinforce your understanding.
Understanding the Basics of Fraction Division
Before diving into the specific problem of 7 1/2 ÷ 3/4, let's review the fundamental principles of fraction division. The core concept revolves around the idea of reciprocals. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 3/4 is 4/3.
The rule for dividing fractions is to multiply the first fraction by the reciprocal of the second fraction. This can be expressed as:
a/b ÷ c/d = a/b × d/c
This seemingly simple rule unlocks the ability to solve complex fraction division problems. Let's apply this to our problem, but first, we need to address the mixed number.
Converting Mixed Numbers to Improper Fractions
The problem presents us with a mixed number, 7 1/2. A mixed number combines a whole number and a fraction. To effectively divide fractions, it's crucial to convert mixed numbers into improper fractions. An improper fraction has a numerator larger than its denominator.
To convert 7 1/2 to an improper fraction, we follow these steps:
- Multiply the whole number by the denominator: 7 x 2 = 14
- Add the numerator: 14 + 1 = 15
- Keep the same denominator: The denominator remains 2.
Therefore, 7 1/2 is equivalent to the improper fraction 15/2.
Method 1: The Reciprocal Method
Now that we've converted 7 1/2 to 15/2, we can apply the reciprocal method to solve 7 1/2 ÷ 3/4 (or 15/2 ÷ 3/4):
- Rewrite the problem: 15/2 ÷ 3/4
- Change division to multiplication: 15/2 × 4/3
- Multiply the numerators: 15 x 4 = 60
- Multiply the denominators: 2 x 3 = 6
- Simplify the result: 60/6 = 10
Therefore, 7 1/2 divided by 3/4 equals 10.
Method 2: Using Long Division with Fractions
While the reciprocal method is generally preferred for its efficiency, understanding long division with fractions offers a deeper insight into the process. This method is particularly helpful for visualizing the division.
- Convert to Improper Fractions (as before): 15/2 ÷ 3/4
- Rewrite as a complex fraction: (15/2) / (3/4)
- Multiply both the numerator and the denominator by the reciprocal of the denominator: [(15/2) x (4/3)] / [(3/4) x (4/3)]
- Simplify: (60/6) / 1 = 10
This method explicitly demonstrates how the reciprocal cancels out the denominator, leaving us with the simplified result.
Method 3: Visualizing the Division
This approach uses a more intuitive method, particularly helpful for beginners who struggle with abstract mathematical concepts. Imagine you have 7 and a half pizzas, and you want to divide them into servings of 3/4 of a pizza each.
- Convert 7 1/2 to quarters: Since 1/4 is half of 1/2, 7 1/2 pizzas contain 30 quarters (7 x 4 = 28 + 2 = 30).
- Divide the quarters: You have 30 quarters of pizza, and each serving is 3 quarters. Dividing 30 by 3 gives you 10 servings.
Therefore, 7 1/2 divided by 3/4 equals 10.
Checking Your Answer: The Importance of Verification
After solving any mathematical problem, especially those involving fractions, it's crucial to verify the answer. One way to do this is to perform the inverse operation: multiplication.
If 7 1/2 divided by 3/4 equals 10, then 10 multiplied by 3/4 should equal 7 1/2. Let's check:
10 x 3/4 = 30/4 = 15/2 = 7 1/2
The verification confirms our answer is correct.
Practical Applications and Real-World Examples
Understanding fraction division isn't just about solving textbook problems; it has numerous practical applications in various fields. Consider these examples:
- Baking: A recipe calls for 3/4 cup of flour per serving, and you want to make 7 1/2 servings. Knowing how to divide 7 1/2 by 3/4 will tell you exactly how much flour you need.
- Construction: Dividing lengths of materials into specific fractional measurements.
- Sewing: Calculating fabric requirements based on fractional pattern measurements.
- Engineering: Precise calculations in designing and constructing various projects often require fraction division.
Expanding Your Understanding: More Complex Fraction Problems
Once you've mastered the division of mixed numbers like 7 1/2 ÷ 3/4, you can move on to more complex scenarios involving:
- Dividing fractions with larger numbers: Practice with larger numerators and denominators to build your confidence and improve your calculation speed.
- Dividing fractions with negative numbers: Understanding how to handle negative signs in fraction division is crucial for more advanced mathematical concepts.
- Dividing fractions involving decimals: This combines fraction and decimal operations, requiring a thorough understanding of both.
- Word problems: Apply your fraction division skills to solve real-world problems described in words, which often involve interpreting the problem correctly before applying the appropriate mathematical operation.
Conclusion: Mastering Fraction Division
Dividing fractions, especially mixed numbers, might initially appear challenging, but by breaking down the process into manageable steps and understanding the underlying principles, it becomes a much more accessible skill. Remember to convert mixed numbers to improper fractions, utilize the reciprocal method for efficient calculation, and always verify your answer. With consistent practice and a willingness to explore different methods, you can confidently master this fundamental mathematical concept and apply it to various real-world situations. The ability to solve problems like 7 1/2 divided by 3/4 opens doors to a deeper understanding of mathematics and its practical applications. Remember to practice regularly – the more you practice, the more comfortable and proficient you will become.
Latest Posts
Latest Posts
-
2 N 3 4n 1
Sep 05, 2025
-
Susan B Anthony Lifes Work
Sep 05, 2025
-
How Are These Ads Similar
Sep 05, 2025
-
The Prepaid Tuition Plan Covers
Sep 05, 2025
-
Ball Rolling Down A Ramp
Sep 05, 2025
Related Post
Thank you for visiting our website which covers about 7 1/2 Divided By 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.