Find The Sum 6/x-4 5/x
gasmanvison
Sep 12, 2025 · 5 min read
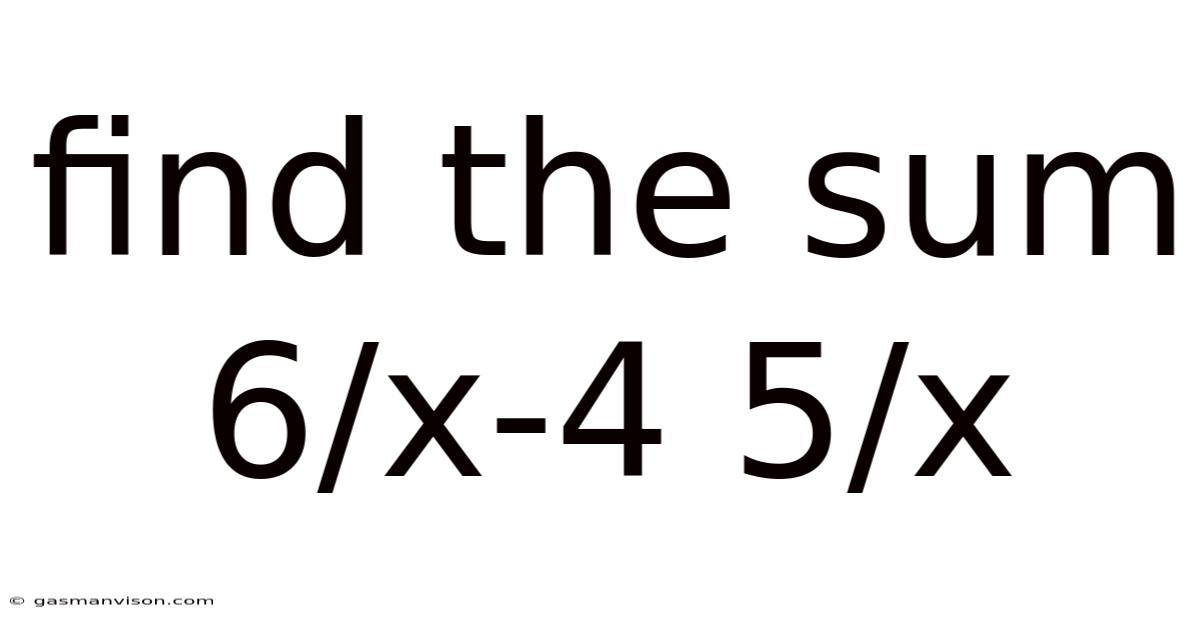
Table of Contents
Finding the Sum of 6/(x-4) and 5/x: A Comprehensive Guide
This article provides a detailed explanation of how to find the sum of the two algebraic fractions, 6/(x-4) and 5/x. We'll cover the fundamental concepts involved, walk through the step-by-step solution, and explore common mistakes to avoid. Understanding this process is crucial for mastering algebraic manipulation and solving more complex equations later on. This guide is suitable for students learning algebra, as well as anyone looking to refresh their understanding of fraction addition.
Meta Description: Learn how to add algebraic fractions with this comprehensive guide. We break down the steps to find the sum of 6/(x-4) and 5/x, covering concepts, solutions, and common pitfalls. Master algebraic manipulation with our detailed explanation.
Understanding the Basics: Adding Fractions
Before tackling the problem, let's review the fundamental principles of adding fractions. The core concept is finding a common denominator. This is a crucial step, as you cannot directly add fractions with different denominators. Think of it like adding apples and oranges – you need to find a common unit before combining them.
For example, to add 1/2 and 1/3, we first find the least common multiple (LCM) of the denominators 2 and 3, which is 6. Then, we rewrite each fraction with the common denominator:
1/2 = 3/6 1/3 = 2/6
Now we can add them: 3/6 + 2/6 = 5/6
The same principle applies to algebraic fractions, but with the added complexity of working with variables.
Finding the Common Denominator for 6/(x-4) and 5/x
Our problem involves the fractions 6/(x-4) and 5/x. To add these, we need to find a common denominator. In this case, the common denominator is simply the product of the two denominators: x(x-4).
This is because neither denominator is a factor of the other. There are no common terms that we can simplify or cancel out beforehand. Therefore, we must multiply each fraction by a suitable form of 1 to obtain the common denominator.
Step-by-Step Solution: Adding the Fractions
-
Find the common denominator: As determined above, the common denominator is x(x-4).
-
Rewrite each fraction with the common denominator:
-
For 6/(x-4), we multiply both the numerator and denominator by x: (6x) / (x(x-4))
-
For 5/x, we multiply both the numerator and denominator by (x-4): (5(x-4)) / (x(x-4))
-
-
Add the numerators: Now that both fractions have the same denominator, we can add their numerators:
(6x) / (x(x-4)) + (5(x-4)) / (x(x-4)) = (6x + 5(x-4)) / (x(x-4))
-
Simplify the numerator: Expand and simplify the expression in the numerator:
(6x + 5x - 20) / (x(x-4)) = (11x - 20) / (x(x-4))
-
Final Result: The sum of 6/(x-4) and 5/x is (11x - 20) / (x(x-4)). This is the simplest form of the expression. Note that this result is only valid for values of x where the denominator is not zero, i.e., x ≠ 0 and x ≠ 4. These values would make the denominator zero and the expression undefined.
Understanding the Restrictions: Excluded Values
It's crucial to understand the restrictions on the variable x. The expression (11x - 20) / (x(x-4)) is undefined when the denominator is equal to zero. This occurs when:
- x = 0
- x - 4 = 0 => x = 4
Therefore, the solution (11x - 20) / (x(x-4)) is valid for all real numbers except x = 0 and x = 4. These values are called excluded values or singularities. Always state these restrictions when working with algebraic fractions to ensure mathematical accuracy.
Common Mistakes to Avoid
Several common mistakes can occur when adding algebraic fractions. Here are some to watch out for:
-
Forgetting to find a common denominator: This is the most fundamental error. You cannot simply add the numerators without a common denominator.
-
Incorrectly multiplying the numerators and denominators: When rewriting fractions with a common denominator, ensure you multiply both the numerator and denominator by the same expression.
-
Errors in simplifying the numerator: Carefully expand and combine like terms in the numerator to avoid arithmetic mistakes.
-
Ignoring excluded values: Always identify and state the values of x that make the denominator zero. Failing to do so can lead to incorrect solutions or undefined expressions.
-
Not simplifying the final answer: After adding the fractions, always check if the resulting expression can be simplified further.
Advanced Applications and Extensions
Understanding the addition of algebraic fractions forms a foundation for tackling more advanced algebraic concepts. These include:
-
Solving rational equations: Equations containing algebraic fractions often require adding or subtracting fractions as a first step.
-
Calculus: Concepts like finding derivatives and integrals often involve manipulating algebraic fractions.
-
Complex fractions: These are fractions where either the numerator or denominator (or both) contains fractions themselves. Mastering the addition of simpler fractions is essential for simplifying complex fractions.
-
Partial fraction decomposition: This technique involves breaking down a complex rational expression into a sum of simpler fractions, often as a necessary step in solving integrals or other problems.
Conclusion
Adding algebraic fractions, such as 6/(x-4) and 5/x, involves finding a common denominator, rewriting the fractions with this common denominator, adding the numerators, simplifying the resulting expression, and finally, stating any restrictions on the variable x to avoid division by zero. By carefully following the steps outlined above and avoiding common pitfalls, you can confidently solve similar problems and build a strong foundation in algebra. Remember to practice regularly to improve your understanding and speed. The more you work with these types of problems, the more intuitive the process will become. This mastery will serve you well in further mathematical studies and applications.
Latest Posts
Latest Posts
-
Molecular Mass Of Sulphuric Acid
Sep 12, 2025
-
Convert 475 Milliliters To Liters
Sep 12, 2025
-
Belief In Justice And Equality
Sep 12, 2025
-
1 1 5 As A Decimal
Sep 12, 2025
-
Proving Vertical Angles Are Congruent
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Find The Sum 6/x-4 5/x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.