Given Abcd Solve For X
gasmanvison
Sep 12, 2025 · 5 min read
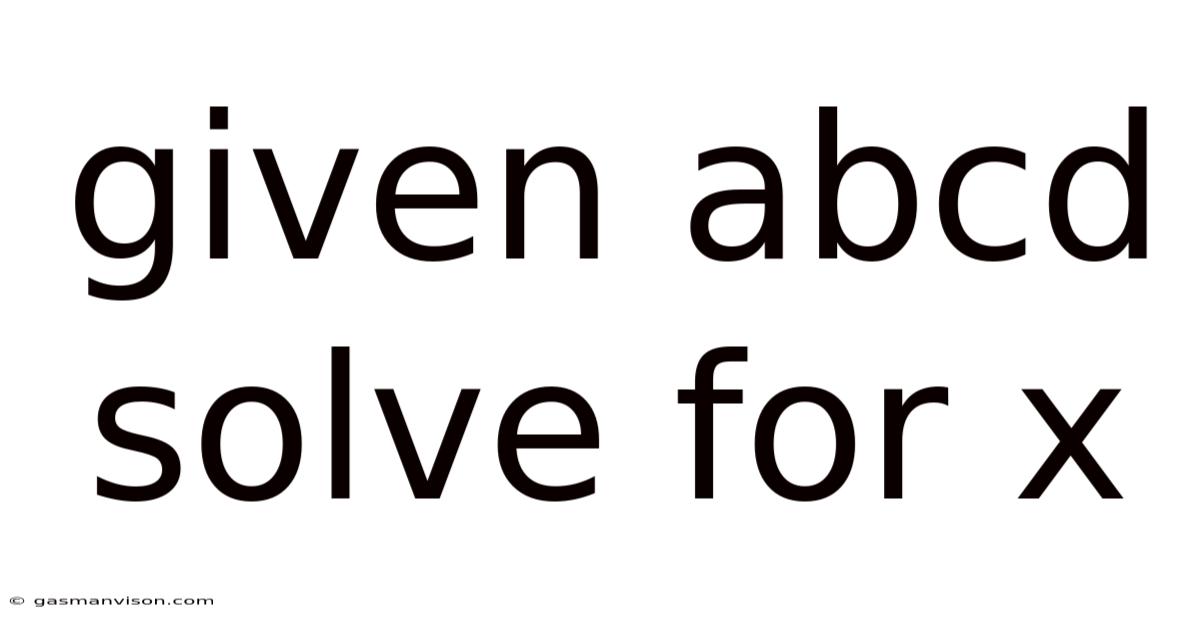
Table of Contents
Solving for X: A Comprehensive Guide to Algebraic Equations
This article provides a comprehensive guide on how to solve for 'x' in various algebraic equations, catering to different levels of mathematical understanding. We'll cover everything from basic linear equations to more complex scenarios, equipping you with the skills and knowledge to confidently tackle these problems. Whether you're a student brushing up on your algebra skills or simply curious about solving for unknowns, this guide will provide a solid foundation.
What does "solve for x" mean?
In mathematics, "solve for x" means to find the value or values of the variable 'x' that make the equation true. The equation represents a relationship between different variables and constants, and solving for 'x' involves isolating 'x' on one side of the equation using algebraic manipulations. This process involves applying inverse operations to both sides of the equation to maintain balance and ultimately find the solution.
Basic Linear Equations: Solving for x with one variable
Let's start with the simplest case: linear equations with one variable. These equations have the general form: ax + b = c, where 'a', 'b', and 'c' are constants, and 'x' is the variable we need to solve for.
Steps to Solve:
-
Isolate the term containing 'x': Subtract 'b' from both sides of the equation:
ax = c - b -
Solve for 'x': Divide both sides by 'a':
x = (c - b) / a
Example:
Solve for x: 3x + 5 = 14
-
Subtract 5 from both sides:
3x = 9 -
Divide both sides by 3:
x = 3
Solving for x in Equations with Multiple Variables
When dealing with equations containing multiple variables, the process becomes slightly more involved, but the fundamental principle remains the same: isolate 'x' using algebraic manipulations.
Example 1: Two Variables
Solve for x: 2x + 3y = 10
In this case, we cannot find a single numerical solution for 'x' without knowing the value of 'y'. The solution will be expressed in terms of 'y':
-
Subtract 3y from both sides:
2x = 10 - 3y -
Divide both sides by 2:
x = 5 - (3/2)y
This shows that the value of x depends on the value of y.
Example 2: Three Variables
Solve for x: 4x + 2y - z = 12
Similar to the previous example, we can express x in terms of y and z:
-
Add z to both sides:
4x + 2y = 12 + z -
Subtract 2y from both sides:
4x = 12 + z - 2y -
Divide both sides by 4:
x = 3 + (z/4) - (y/2)
Solving for x in Quadratic Equations
Quadratic equations are equations of the form ax² + bx + c = 0, where 'a', 'b', and 'c' are constants and 'a' is not equal to zero. Solving for 'x' in quadratic equations requires more advanced techniques.
Methods for Solving Quadratic Equations:
-
Factoring: This method involves expressing the quadratic equation as a product of two linear factors. If we can factor the equation into (px + q)(rx + s) = 0, then the solutions for x are x = -q/p and x = -s/r.
-
Quadratic Formula: This formula provides a direct solution for x:
x = [-b ± √(b² - 4ac)] / 2a
The expression b² - 4ac is called the discriminant. It determines the nature of the roots:
* If b² - 4ac > 0, there are two distinct real roots.
* If b² - 4ac = 0, there is one real root (repeated root).
* If b² - 4ac < 0, there are two complex roots.
- Completing the Square: This method involves manipulating the equation to create a perfect square trinomial, which can then be easily factored.
Example:
Solve for x: x² + 5x + 6 = 0
Factoring: This equation can be factored as (x + 2)(x + 3) = 0. Therefore, x = -2 or x = -3.
Quadratic Formula: Using the quadratic formula with a = 1, b = 5, and c = 6:
x = [-5 ± √(5² - 4 * 1 * 6)] / 2 * 1
x = [-5 ± √1] / 2
x = (-5 + 1) / 2 = -2 or x = (-5 - 1) / 2 = -3
Solving for x in Exponential Equations
Exponential equations involve variables in the exponent. Solving these requires using logarithmic properties.
Example:
Solve for x: 2ˣ = 8
We can rewrite 8 as 2³:
2ˣ = 2³
Since the bases are equal, the exponents must be equal:
x = 3
Solving for x in Logarithmic Equations
Logarithmic equations involve logarithms of variables. These are solved using the properties of logarithms.
Example:
Solve for x: log₂(x) = 3
Using the definition of a logarithm, this equation can be rewritten as:
2³ = x
Therefore, x = 8
Solving Systems of Equations for x
When dealing with multiple equations involving 'x' and other variables, we need to solve a system of equations. Common methods include:
-
Substitution: Solve one equation for 'x' in terms of other variables and substitute this expression into the other equation(s).
-
Elimination: Multiply the equations by constants to eliminate one variable, then solve for the remaining variable.
Example (Substitution):
Solve for x:
x + y = 5
2x - y = 4
Solve the first equation for y: y = 5 - x
Substitute this into the second equation: 2x - (5 - x) = 4
Simplify and solve for x: 3x = 9, therefore x = 3
Example (Elimination):
Solve for x:
x + y = 5
x - y = 1
Add the two equations together: 2x = 6, therefore x = 3
Advanced Techniques and Considerations:
Solving for 'x' in more complex equations may require advanced techniques like:
- Partial Fraction Decomposition: Used to simplify rational functions before solving.
- Numerical Methods: Approximation techniques used for equations that are difficult or impossible to solve analytically. These include methods like the Newton-Raphson method.
Conclusion:
Solving for 'x' is a fundamental skill in algebra and mathematics. This comprehensive guide has covered various methods and techniques, progressing from basic linear equations to more complex scenarios involving quadratic, exponential, and logarithmic equations, as well as systems of equations. Understanding these methods will equip you with the tools to confidently tackle a wide range of algebraic problems. Remember to practice regularly to solidify your understanding and improve your problem-solving skills. The key is to systematically apply algebraic manipulations to isolate 'x' and find the solution that satisfies the given equation.
Latest Posts
Latest Posts
-
Molar Mass Of Glucose C6h12o6
Sep 12, 2025
-
How Many Weeks A Year
Sep 12, 2025
-
How Many Inches Is 13cm
Sep 12, 2025
-
Does Ice Cream Have Algae
Sep 12, 2025
-
200g Of Sugar Into Cups
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Given Abcd Solve For X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.