How Many 1/2 Is 3/4
gasmanvison
Sep 09, 2025 · 5 min read
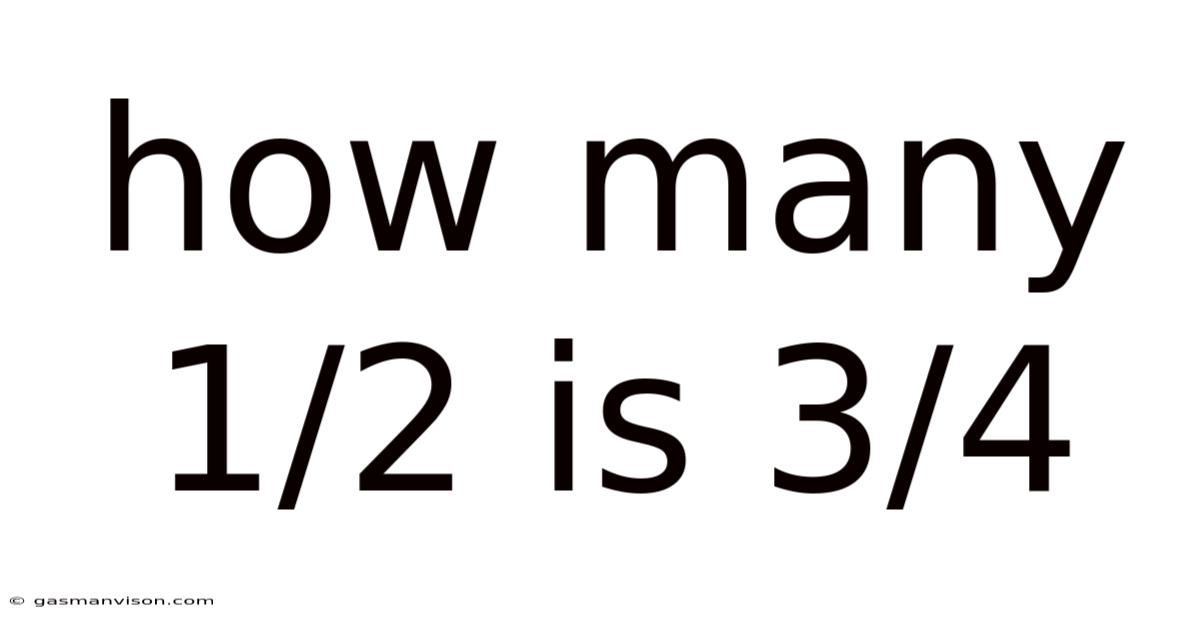
Table of Contents
How Many Halves Make Three-Quarters? A Deep Dive into Fractions
This seemingly simple question, "How many 1/2 is 3/4?", delves into the fundamental concepts of fractions, offering a valuable opportunity to explore various mathematical approaches and strengthen our understanding of fractional arithmetic. While the answer might appear immediately obvious to some, a comprehensive exploration reveals a richer understanding of equivalent fractions, division of fractions, and the relationship between numerators and denominators. This article will guide you through multiple methods to solve this problem, offering explanations suitable for various levels of mathematical understanding. We'll also explore practical applications and further solidify your knowledge of fractions.
Understanding the Question: Deconstructing the Problem
The question, "How many 1/2 is 3/4?", essentially asks us to determine how many times the fraction 1/2 is contained within the fraction 3/4. This translates to a division problem: 3/4 ÷ 1/2. Understanding this fundamental translation is crucial to solving the problem effectively. We're not simply looking for an equivalent fraction; we're exploring the relationship between two different fractions.
Method 1: Visual Representation – The Power of Pictorial Understanding
A visual representation can often clarify complex mathematical concepts. Imagine a pizza cut into four equal slices. Three-quarters (3/4) represents three of these slices. Now, consider a half (1/2) – this would represent two of these slices. By visually comparing the two, we can easily see that 3/4 contains only one and a half (1 1/2) halves.
This method, while intuitive, is limited in its applicability to more complex fractions. However, it establishes a strong foundational understanding of the relationship between 3/4 and 1/2.
Method 2: Converting to Common Denominators – The Foundation of Fraction Comparison
One of the most fundamental techniques in fraction arithmetic is converting fractions to a common denominator. This allows for direct comparison and easier manipulation.
-
Find a Common Denominator: The least common denominator (LCD) of 2 and 4 is 4.
-
Convert Fractions: 1/2 can be converted to an equivalent fraction with a denominator of 4 by multiplying both the numerator and the denominator by 2: (1 x 2) / (2 x 2) = 2/4.
-
Compare Fractions: Now we can easily compare 3/4 and 2/4. We can see that 3/4 is 1.5 times larger than 2/4 (3/4 / 2/4 = 1.5). Therefore, there are 1.5 halves in three-quarters.
Method 3: Division of Fractions – A Formal Mathematical Approach
This method utilizes the formal mathematical process of dividing fractions. Recall that dividing by a fraction is the same as multiplying by its reciprocal.
-
Rewrite the Problem: The problem "How many 1/2 is 3/4?" can be rewritten as a division problem: 3/4 ÷ 1/2.
-
Find the Reciprocal: The reciprocal of 1/2 is 2/1 (or simply 2).
-
Multiply: Change the division to multiplication by using the reciprocal of the second fraction: 3/4 x 2/1.
-
Simplify: Multiply the numerators (3 x 2 = 6) and the denominators (4 x 1 = 4): 6/4.
-
Reduce: Simplify the resulting fraction by dividing both the numerator and the denominator by their greatest common divisor, which is 2: 6/4 = 3/2.
-
Convert to a Mixed Number: The improper fraction 3/2 can be converted into a mixed number: 1 1/2.
Therefore, there are 1 1/2 halves in three-quarters. This method provides a robust and generalizable approach suitable for solving similar problems with more complex fractions.
Method 4: Using Decimal Equivalents – An Alternative Perspective
Converting fractions to decimals can offer a different perspective on the problem.
-
Convert to Decimals: 3/4 = 0.75 and 1/2 = 0.5.
-
Divide: Divide the decimal equivalent of 3/4 by the decimal equivalent of 1/2: 0.75 ÷ 0.5 = 1.5.
This confirms our previous findings that there are 1.5 halves in three-quarters. This method is particularly useful when working with fractions that are easily converted to terminating decimals.
Practical Applications and Real-World Examples
Understanding how to solve this type of fractional problem has various real-world applications:
-
Cooking and Baking: Recipes often call for fractional measurements. Knowing how many halves are in three-quarters is crucial for accurate ingredient measurements. Imagine a recipe requiring 3/4 cup of flour, and you only have a 1/2 cup measuring cup. Understanding the relationship between these fractions would help you accurately measure the required flour.
-
Construction and Engineering: Precision is paramount in construction and engineering. Working with fractional dimensions requires a solid understanding of fractional arithmetic. Calculations involving lengths, areas, and volumes often involve fractions, and the ability to convert and compare them is critical.
-
Finance and Budgeting: Managing finances often involves working with fractional amounts of money. Understanding fractional relationships is essential for accurate budgeting and financial planning.
-
Data Analysis: In data analysis, representing and comparing data using fractions and percentages is common. Understanding fractional relationships helps in interpreting and comparing data effectively.
Expanding the Concept: Beyond Halves and Three-Quarters
The principles explored in solving "How many 1/2 is 3/4?" are applicable to a wide range of fractional problems. The same methods – visual representation, common denominators, division of fractions, and decimal conversion – can be used to solve similar problems involving different fractions. Consider these examples:
- How many 1/3 is 2/9?
- How many 2/5 is 4/15?
- How many 3/8 is 9/16?
By applying the techniques discussed above, you can confidently solve these and many more complex fractional problems.
Conclusion: Mastering Fractions – A Building Block for Mathematical Proficiency
The seemingly simple question, "How many 1/2 is 3/4?", offers a valuable opportunity to reinforce our understanding of fundamental fractional concepts. Through visual representation, common denominator conversion, formal division of fractions, and decimal equivalence, we've explored multiple approaches to solving this problem. Mastering these techniques empowers us to tackle more complex fractional arithmetic with confidence, leading to a stronger foundation in mathematics and its diverse real-world applications. The ability to comfortably work with fractions is a crucial skill applicable across numerous disciplines, demonstrating the importance of a thorough understanding of these fundamental concepts. By understanding the relationships between fractions and applying the various methods outlined above, you'll be well-equipped to confidently handle any fractional problem you encounter.
Latest Posts
Latest Posts
-
Gcf Of 40 And 24
Sep 09, 2025
-
Exercise 19 Problems Part 2
Sep 09, 2025
-
Pretty Is To Beautiful As
Sep 09, 2025
-
Bright Red Gills Fish Delivery
Sep 09, 2025
-
750 Ml To Fl Ounces
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about How Many 1/2 Is 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.