Multiply 2.9 X And 5x
gasmanvison
Sep 08, 2025 · 5 min read
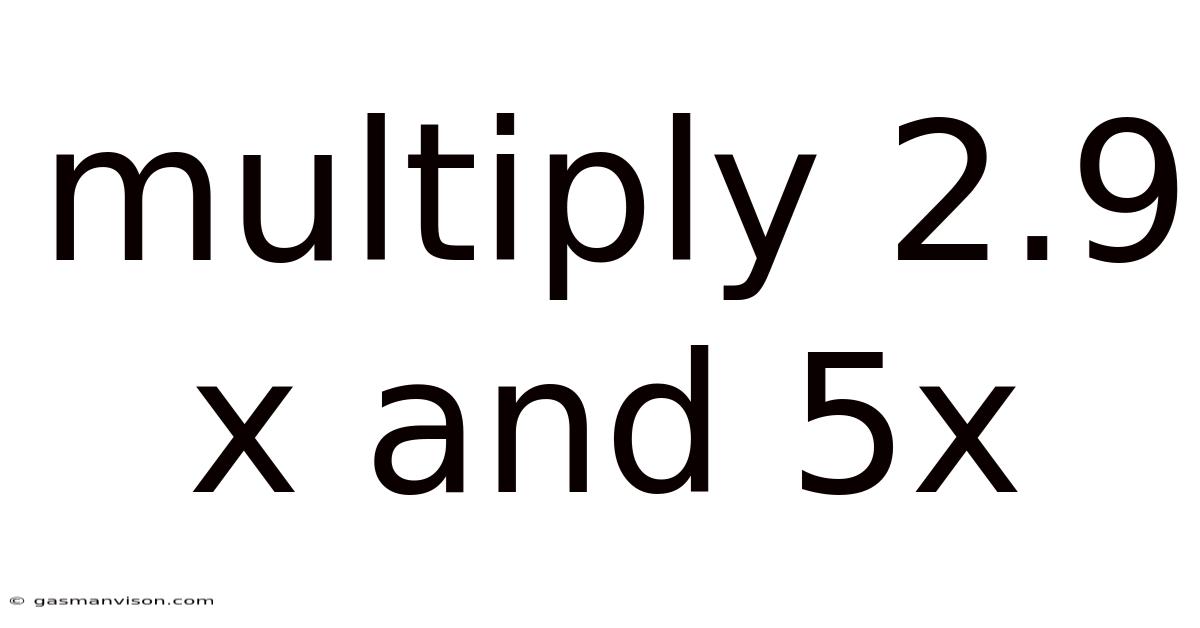
Table of Contents
Multiplying 2.9x and 5x: A Deep Dive into Algebraic Expressions
This article explores the seemingly simple yet fundamentally important algebraic operation of multiplying 2.9x and 5x. While the calculation itself is straightforward, understanding the underlying principles and potential applications offers valuable insights into algebra and its role in various fields. We'll delve into the process, discuss common pitfalls, and explore advanced applications to solidify your understanding. This guide is perfect for students learning algebra, those brushing up on their skills, or anyone curious about the power of algebraic manipulation.
Meta Description: Learn how to multiply algebraic expressions, specifically 2.9x and 5x. This in-depth guide covers the process, addresses common mistakes, and explores advanced applications relevant to various fields. Master algebraic multiplication with this comprehensive tutorial.
Understanding the Basics: Coefficients and Variables
Before diving into the multiplication, let's review fundamental algebraic concepts. In the expressions 2.9x and 5x, we have two key components:
-
Coefficients: These are the numerical values preceding the variable. In our example, 2.9 and 5 are the coefficients. They represent the quantitative scaling of the variable.
-
Variables: The 'x' represents a variable, an unknown quantity that can take on different values. Variables are crucial for representing generalized relationships and solving equations.
Multiplying the Expressions: A Step-by-Step Approach
Multiplying 2.9x and 5x involves two distinct steps:
-
Multiply the coefficients: Multiply the numerical coefficients together: 2.9 * 5 = 14.5
-
Combine the variables: Multiply the variables together: x * x = x². Remember, when you multiply variables with the same base, you add their exponents (in this case, x has an implied exponent of 1, so 1 + 1 = 2).
Therefore, the product of 2.9x and 5x is 14.5x².
Illustrative Examples: Real-World Applications
While the multiplication itself might seem abstract, understanding its application in real-world scenarios is crucial. Let's consider a few examples:
-
Area Calculation: Imagine you have a rectangular garden. One side measures 2.9x meters and the other measures 5x meters. To calculate the area (Area = length * width), you'd multiply these expressions: (2.9x) * (5x) = 14.5x². This means the area of the garden is 14.5 times the square of 'x'. If 'x' represents 10 meters, for instance, the area would be 14.5 * 10² = 1450 square meters.
-
Volume Calculation: Consider a cuboid with dimensions 2.9x, 5x, and 'y' meters. The volume (Volume = length * width * height) would be calculated as (2.9x) * (5x) * y = 14.5x²y cubic meters. This formula allows you to calculate the volume for any value of 'x' and 'y'.
-
Physics and Engineering: Algebraic multiplication of variables frequently occurs in physics and engineering equations. For instance, in calculating kinetic energy (KE = 1/2 * mv²), if the mass (m) is represented by 2.9x and the velocity (v) is 5x, then the kinetic energy becomes 1/2 * (2.9x) * (5x)² = 36.25x³.
Expanding the Concept: Polynomials and Beyond
The principles demonstrated in multiplying 2.9x and 5x extend to more complex algebraic expressions involving polynomials. A polynomial is an expression consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables.
Consider multiplying (2.9x + 3) and (5x - 2). This requires using the distributive property (also known as the FOIL method):
(2.9x + 3)(5x - 2) = (2.9x)(5x) + (2.9x)(-2) + (3)(5x) + (3)(-2) = 14.5x² - 5.8x + 15x - 6 = 14.5x² + 9.2x - 6
This example highlights the importance of carefully applying the distributive property to ensure accurate expansion of the polynomial expression.
Common Mistakes and How to Avoid Them
Several common mistakes can occur when multiplying algebraic expressions. Understanding these helps avoid errors:
-
Forgetting to multiply both the coefficients and the variables: Remember, both the numerical and the variable parts must be multiplied. Ignoring one leads to an incorrect result.
-
Incorrectly adding exponents: When multiplying variables with the same base (e.g., x * x), add the exponents, not multiply them. x * x = x², not x².
-
Neglecting the order of operations: Follow the order of operations (PEMDAS/BODMAS) correctly. Parentheses, exponents, multiplication and division (from left to right), addition and subtraction (from left to right).
-
Errors in the distributive property: Carefully apply the distributive property when expanding expressions involving multiple terms. Ensure each term in the first expression is multiplied by each term in the second.
Advanced Applications and Further Exploration
The fundamental principles discussed in this article form the basis for more advanced algebraic concepts:
-
Solving Quadratic Equations: The resulting expression 14.5x² often appears in quadratic equations, which are equations of the form ax² + bx + c = 0. Solving these equations involves techniques like factoring, completing the square, or using the quadratic formula.
-
Calculus: In calculus, differentiation and integration involve manipulating algebraic expressions. Understanding the multiplication of expressions is essential for calculating derivatives and integrals.
-
Linear Algebra: Linear algebra deals with vectors, matrices, and linear transformations. Many operations in linear algebra involve multiplying algebraic expressions representing vectors and matrices.
-
Computer Science: Algebraic expressions are fundamental in computer programming and algorithm design. They are used to model various computational processes and solve complex problems.
Conclusion: Mastering Algebraic Multiplication
Multiplying 2.9x and 5x, while seemingly simple, serves as a cornerstone of algebraic manipulation. Understanding the principles involved—coefficient multiplication, variable combination, and the distributive property—is essential for success in algebra and its applications across numerous fields. By carefully applying these principles and avoiding common pitfalls, you can confidently tackle more complex algebraic expressions and solve real-world problems involving variables and equations. This knowledge forms the foundation for progressing to more advanced mathematical concepts and problem-solving techniques. Continued practice and exploration of these concepts will solidify your understanding and build your algebraic proficiency.
Latest Posts
Latest Posts
-
Area Of 6 Inch Circle
Sep 08, 2025
-
Legal Drinking Age Date Today
Sep 08, 2025
-
What Is 40 Of 120
Sep 08, 2025
-
5 Square Root Of 3
Sep 08, 2025
-
Automobile Bicycle Collisions Usually Occur Because
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about Multiply 2.9 X And 5x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.