Simplify 1 2x 1 2
gasmanvison
Sep 15, 2025 · 5 min read
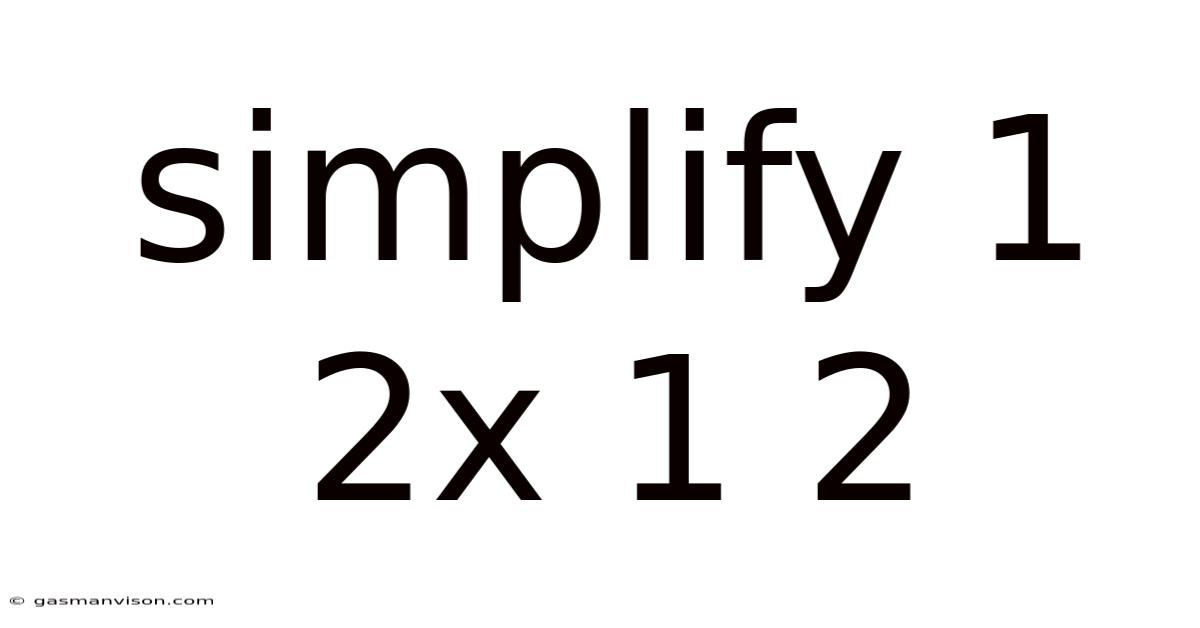
Table of Contents
Simplifying 1/(2x + 1/2): A Comprehensive Guide
This article delves into the simplification of the algebraic expression 1/(2x + 1/2), exploring various methods and providing a step-by-step approach suitable for students and anyone looking to improve their algebraic skills. We will cover simplifying fractions, dealing with complex fractions, and applying the principles of order of operations (PEMDAS/BODMAS). This guide emphasizes a thorough understanding of the process, not just the final answer. Understanding the why behind each step is crucial for mastering algebraic simplification.
Meta Description: Learn how to simplify the algebraic expression 1/(2x + 1/2) with this comprehensive guide. We cover fraction simplification, complex fraction handling, and order of operations, providing a step-by-step solution and explanations. Improve your algebraic skills today!
The expression 1/(2x + 1/2) is a classic example of a complex fraction, meaning it contains fractions within a fraction. Successfully simplifying this requires a clear understanding of several key algebraic concepts:
1. Understanding the Order of Operations (PEMDAS/BODMAS)
Before we begin simplification, it's crucial to remember the order of operations. PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction) dictate the sequence in which operations should be performed. In this case, the parentheses (or brackets) take precedence. Therefore, we must first simplify the expression within the denominator (2x + 1/2) before addressing the overall fraction.
2. Finding a Common Denominator within the Denominator
The expression within the denominator, (2x + 1/2), contains a whole number (2x) and a fraction (1/2). To combine these terms, we need a common denominator. The common denominator for 2x and 1/2 is 2. We can rewrite 2x as (4x)/2.
Therefore, (2x + 1/2) becomes ((4x)/2 + 1/2). Now we can combine the fractions:
((4x)/2 + 1/2) = (4x + 1)/2
3. Rewriting the Original Expression
Now that we have simplified the denominator, we can rewrite the original expression:
1/(2x + 1/2) becomes 1/((4x + 1)/2)
4. Simplifying Complex Fractions
This is where many students encounter difficulty. A complex fraction, such as 1/((4x + 1)/2), can be simplified by remembering that dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of (4x + 1)/2 is 2/(4x + 1).
Therefore, we can rewrite the expression as:
1 * (2/(4x + 1))
This simplifies to:
2/(4x + 1)
5. Final Simplified Expression
The fully simplified expression of 1/(2x + 1/2) is 2/(4x + 1). This is the most concise and simplified form of the original expression. It's important to note that this simplification is valid for all values of 'x' except for x = -1/4, where the denominator would become zero, resulting in an undefined expression.
Alternative Approach: Using a Common Denominator for the Entire Expression
While the previous method is straightforward, there's an alternative approach that uses a common denominator from the beginning. This might feel slightly more intuitive for some:
-
Find a Common Denominator: Observe that the entire expression involves the number 2 in the denominator. Let's multiply the numerator and denominator of the entire fraction by 2:
(2 * 1) / (2 * (2x + 1/2))
-
Simplify: This simplifies to:
2 / (4x + 1)
This method arrives at the same simplified expression, 2/(4x + 1), showcasing that different algebraic strategies can lead to the same correct result.
Further Exploration and Applications
Understanding this type of simplification is crucial for numerous applications in:
- Calculus: Simplifying complex fractions is often a necessary step in differentiating and integrating functions.
- Physics and Engineering: Many physical formulas and equations involve fractions and require simplification for practical application.
- Financial Modeling: Complex financial models often require simplifying complex expressions involving fractions to make calculations easier.
- Computer Science: Algorithmic efficiency often requires simplifying mathematical expressions to reduce computational complexity.
Common Mistakes to Avoid
- Ignoring the Order of Operations: Always follow PEMDAS/BODMAS to ensure accurate simplification. Failing to do so can lead to significant errors.
- Incorrectly Handling Reciprocals: Remember that the reciprocal of a fraction is obtained by swapping the numerator and denominator. Mistakes in this step are common.
- Forgetting to Check for Undefined Values: Always check if there are any values of the variable that would make the denominator zero. In this case, x = -1/4 would make the denominator zero, rendering the expression undefined.
- Not Simplifying Completely: Always ensure the expression is in its most simplified form. There might be common factors in the numerator and denominator that can be canceled out.
Practice Problems
To solidify your understanding, try simplifying the following expressions using the methods described above:
- 3/(x + 1/3)
- 1/(5x - 2/5)
- (2x + 1)/(x + 1/2)
- (1/x + 1/y)/ (1/x - 1/y)
- 1/(1/x + 1/y)
By working through these problems, you'll gain confidence and proficiency in simplifying complex algebraic expressions. Remember to always show your work, step-by-step, to identify and correct any potential errors. Consistent practice is key to mastering algebraic simplification.
This comprehensive guide has provided a detailed exploration of how to simplify the algebraic expression 1/(2x + 1/2). We've explored multiple methods, highlighted common pitfalls, and encouraged further practice. By understanding the underlying principles of order of operations, common denominators, and reciprocal fractions, you can confidently tackle similar complex fraction simplifications in various mathematical and scientific contexts. Remember to always check your work for accuracy and ensure the final expression is completely simplified.
Latest Posts
Latest Posts
-
Motorists Driving Large Trucks Shoud
Sep 15, 2025
-
16 Oz Is A Lb
Sep 15, 2025
-
What Is 2 5 Equivalent To
Sep 15, 2025
-
90 Confidence Interval Z Score
Sep 15, 2025
-
How Do You Spell Vicious
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Simplify 1 2x 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.