Simplify 3x 2 3x 2
gasmanvison
Sep 15, 2025 · 5 min read
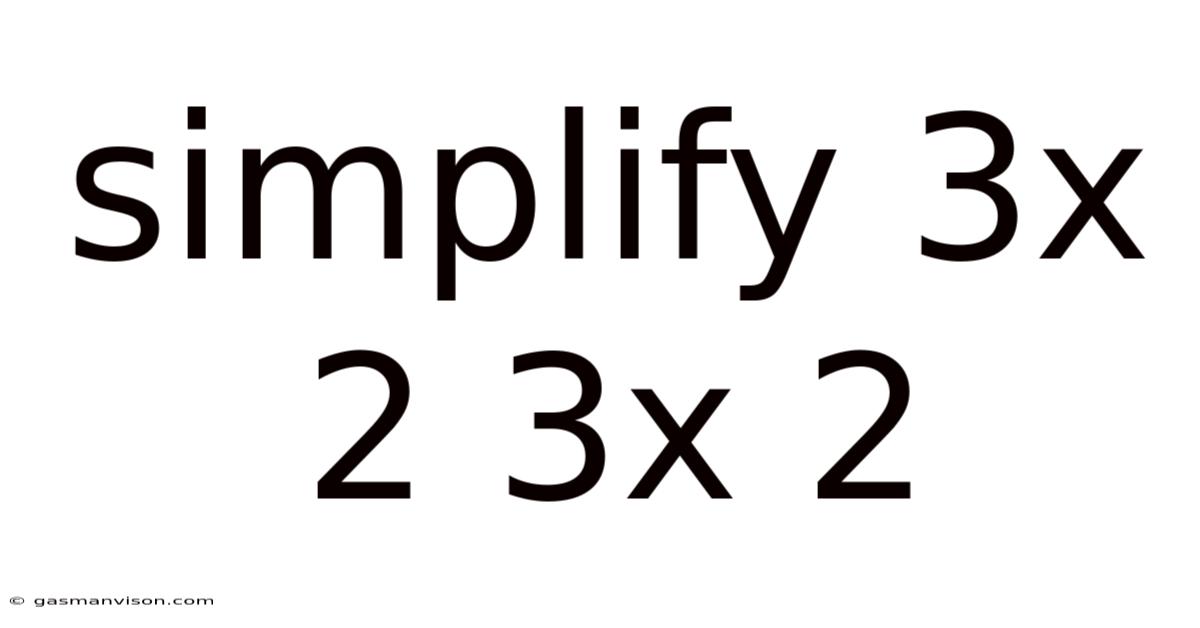
Table of Contents
Simplifying 3x² + 3x²: A Comprehensive Guide to Algebraic Expressions
This article delves into the seemingly simple, yet fundamentally important, task of simplifying the algebraic expression 3x² + 3x². While the problem itself might appear trivial at first glance, understanding the underlying principles involved lays a crucial foundation for more complex algebraic manipulations. We'll explore the concept of like terms, the distributive property, and the significance of this simplification in broader mathematical contexts. This guide will be particularly beneficial for students learning algebra, but it also serves as a valuable refresher for anyone looking to sharpen their mathematical skills.
Meta Description: Learn how to simplify the algebraic expression 3x² + 3x² through a comprehensive guide covering like terms, the distributive property, and practical applications in algebra. This detailed explanation makes simplifying algebraic expressions easier for beginners and a helpful refresher for experienced learners.
Understanding Like Terms
Before diving into the simplification process, let's clarify the concept of like terms. Like terms are terms in an algebraic expression that have the same variable(s) raised to the same power(s). In our expression, 3x² + 3x², both terms share the same variable, 'x', raised to the same power, 2. This makes them like terms. Contrast this with expressions like 3x² + 3x or 3x² + 3y², where the terms are not alike because the variables and/or their powers differ. Identifying like terms is the crucial first step in simplifying algebraic expressions.
The Power of Combining Like Terms
The core principle behind simplifying 3x² + 3x² rests on the ability to combine like terms. Since both terms are identical, we can think of it as adding three of something to another three of the same thing. If we were dealing with apples, for instance, 3 apples + 3 apples = 6 apples. The same logic applies to algebraic terms. The 'x²' acts as the 'apple' in our analogy; it's the common element.
Therefore, 3x² + 3x² simplifies to 6x². We add the numerical coefficients (the numbers in front of the variable) while keeping the variable and its exponent unchanged.
The Distributive Property: An Alternative Approach
While directly combining like terms is the most efficient method for this specific problem, it’s helpful to understand how the distributive property can also be applied. The distributive property states that a(b + c) = ab + ac. Although not immediately apparent in this case, we can rewrite the expression to illustrate this principle:
We can factor out the common term, x², from both terms:
x²(3 + 3)
Now, applying the distributive property in reverse, we simplify the expression within the parentheses:
x²(6) = 6x²
This demonstrates that the distributive property, a fundamental concept in algebra, leads to the same simplified result. This method becomes more useful when dealing with more complex expressions involving multiple like terms.
Practical Applications and Extensions
Simplifying algebraic expressions like 3x² + 3x² is not an isolated skill; it's a building block for more advanced mathematical operations. Here are some examples of where this fundamental skill becomes indispensable:
-
Solving Equations: Many algebraic equations require simplification before solutions can be found. Consider the equation 3x² + 3x² = 12. Simplifying the left-hand side to 6x² allows us to easily solve for x.
-
Graphing Quadratic Functions: Quadratic functions, represented by equations like y = ax² + bx + c, often involve simplifying expressions before graphing. Simplifying like terms is crucial for determining the vertex, intercepts, and overall shape of the parabola.
-
Calculus: In calculus, simplifying expressions is essential for differentiation and integration. Complex expressions often need to be simplified before applying calculus techniques.
-
Physics and Engineering: Many physical phenomena are modeled using algebraic equations. Simplifying expressions is crucial for deriving meaningful results and understanding the relationships between different variables.
Expanding on the Concept: More Complex Examples
Let's extend our understanding by considering slightly more complex examples:
Example 1: 5x³ + 2x³ - x³
Here, we have three like terms, all involving x³:
5x³ + 2x³ - x³ = (5 + 2 - 1)x³ = 6x³
We simply add and subtract the coefficients, maintaining the x³ term.
Example 2: 2x²y + 4x²y - 3x²y
This example introduces a second variable, y, but the like terms share the same variables raised to the same powers (x²y). Thus, we proceed similarly:
2x²y + 4x²y - 3x²y = (2 + 4 - 3)x²y = 3x²y
Example 3: 4x² + 2x + 3x² + 5x
This example involves two sets of like terms: those with x² and those with x. We simplify them separately:
4x² + 3x² + 2x + 5x = (4 + 3)x² + (2 + 5)x = 7x² + 7x
Here, we cannot combine 7x² and 7x because they are not like terms (different exponents).
Avoiding Common Mistakes
While simplifying algebraic expressions seems straightforward, some common pitfalls can lead to errors:
-
Ignoring the Signs: Pay close attention to the signs (+ or -) preceding each term. Incorrectly handling negative signs is a frequent source of mistakes.
-
Misinterpreting Exponents: Ensure that you are only combining terms with the exact same variables and exponents. x² and x are not like terms.
-
Incorrectly Combining Unlike Terms: Remember to only combine like terms. Attempting to combine unlike terms will lead to an incorrect simplified expression.
Conclusion: Mastering the Fundamentals
Simplifying the expression 3x² + 3x² to 6x² may appear elementary, but it encapsulates fundamental algebraic concepts that form the backbone of more advanced mathematical operations. By understanding like terms, applying the distributive property, and practicing with increasingly complex examples, you build a solid foundation for success in algebra and beyond. Mastering this skill enhances your problem-solving abilities and unlocks the door to more sophisticated mathematical explorations. Remember the importance of paying attention to details, handling signs correctly, and accurately identifying like terms to avoid common mistakes. With consistent practice, simplifying algebraic expressions becomes second nature, paving the way for tackling more challenging mathematical problems with confidence.
Latest Posts
Latest Posts
-
With Optionally Renewable Health Policies
Sep 15, 2025
-
120 Days How Many Months
Sep 15, 2025
-
Busco Una Orquesta Que Salsa
Sep 15, 2025
-
X 2 2x 8 0
Sep 15, 2025
-
How Many Letters In Supercalifragilisticexpialidocious
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Simplify 3x 2 3x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.