Simplify 8x - 9x Completely
gasmanvison
Sep 22, 2025 · 5 min read
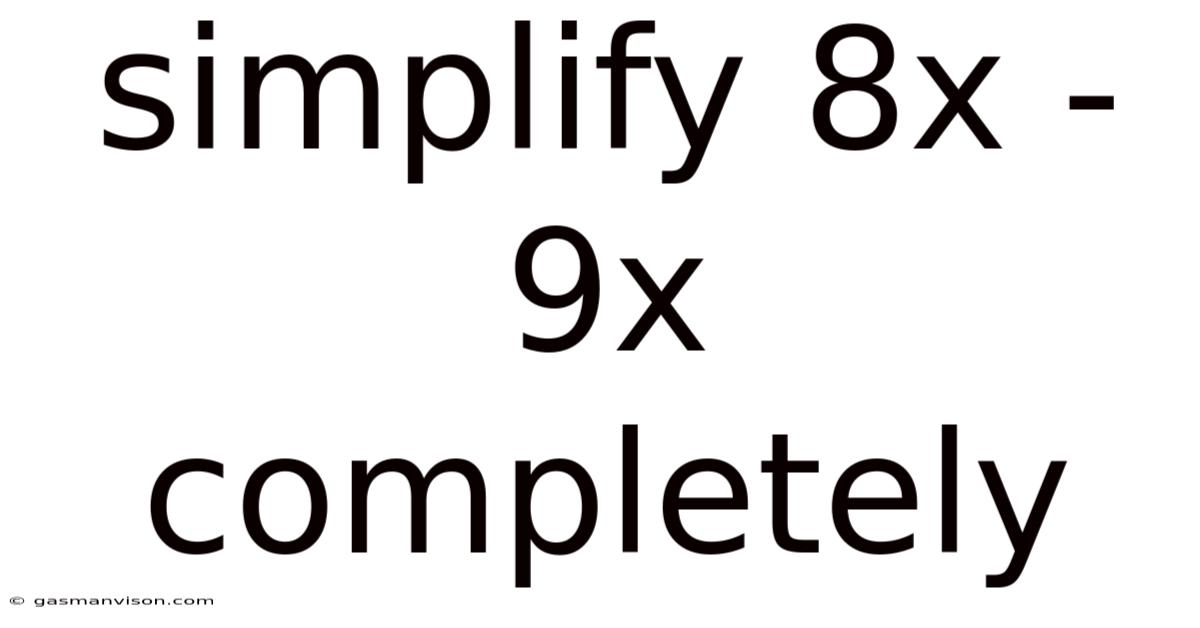
Table of Contents
Simplifying Algebraic Expressions: A Deep Dive into 8x - 9x
This article will delve into the seemingly simple algebraic expression, 8x - 9x, providing a comprehensive explanation that goes beyond just the answer. We'll explore the fundamental concepts of algebra, the rules governing simplification, and practical applications to build a strong understanding of this foundational concept. Understanding this seemingly simple equation is crucial for mastering more complex algebraic manipulations later on. This guide will serve as a complete resource for anyone learning algebra, from beginners to those seeking a refresher.
What is an Algebraic Expression?
Before we dive into simplifying 8x - 9x, let's establish a clear understanding of algebraic expressions. An algebraic expression is a mathematical phrase that combines numbers, variables, and operators. Variables are usually represented by letters (like x, y, z) that stand in for unknown values. Operators are symbols that indicate mathematical operations, such as addition (+), subtraction (-), multiplication (× or *), and division (÷ or /). For example, 3x + 5, 2y - 7, and 4ab are all algebraic expressions.
Understanding Terms and Coefficients
In an algebraic expression, each part separated by a plus or minus sign is called a term. In the expression 8x - 9x, we have two terms: 8x and -9x.
Within each term, the number multiplied by the variable is called the coefficient. In 8x, the coefficient is 8, and in -9x, the coefficient is -9. The variable itself (x in this case) represents an unknown quantity. It's crucial to understand that the negative sign is attached to the coefficient, not just the variable.
The Fundamentals of Simplifying Algebraic Expressions
Simplifying an algebraic expression means rewriting it in its most concise form without changing its value. This typically involves combining like terms. Like terms are terms that have the same variables raised to the same powers. For example, 3x and 5x are like terms, but 3x and 3x² are not.
The process of simplification relies on the distributive property, which states that a(b + c) = ab + ac. This property allows us to factor out common variables or coefficients to combine like terms.
Simplifying 8x - 9x: A Step-by-Step Guide
Now, let's tackle the simplification of 8x - 9x. Since both terms are like terms (they both contain the variable x raised to the power of 1), we can combine them. We do this by adding or subtracting their coefficients.
-
Identify Like Terms: Both 8x and -9x are like terms because they both contain the variable 'x' raised to the power of 1.
-
Combine Coefficients: Add the coefficients: 8 + (-9) = -1
-
Write the Simplified Expression: The simplified expression is -1x, or more commonly written as -x.
Therefore, 8x - 9x simplifies to -x.
Illustrative Examples: Expanding the Concept
Let's explore similar examples to solidify our understanding.
-
Example 1: 5y + 2y - y: Here, we have three like terms, all containing the variable 'y'. Combining the coefficients: 5 + 2 - 1 = 6. Therefore, the simplified expression is 6y.
-
Example 2: 3a - 7a + 10a - a: Again, all terms are like terms with the variable 'a'. Combining coefficients: 3 - 7 + 10 - 1 = 5. The simplified expression is 5a.
-
Example 3: 2xy + 5xy - 3xy: In this example, the like terms are 2xy, 5xy, and -3xy. Combining the coefficients gives us: 2 + 5 - 3 = 4. The simplified expression is 4xy.
These examples demonstrate the consistent application of the principle of combining like terms by adding or subtracting their coefficients.
Understanding the Concept of Zero
It's important to note the case when the coefficients cancel each other out completely. For example:
- Example 4: 6z - 6z: Combining coefficients results in 6 - 6 = 0. Therefore, the simplified expression is 0.
This illustrates that the expression simplifies to zero, meaning the original expression is equal to zero regardless of the value of 'z'.
Practical Applications and Real-World Scenarios
Simplifying algebraic expressions is a fundamental skill in various fields, including:
-
Physics: Calculating forces, velocities, and accelerations often involves manipulating algebraic expressions.
-
Engineering: Designing structures, circuits, and systems requires solving equations involving variables and simplifying expressions to make them manageable.
-
Economics: Analyzing costs, profits, and market trends often requires manipulating algebraic expressions to model relationships between variables.
-
Computer Science: Algorithm design and optimization frequently involve simplifying expressions to increase efficiency.
-
Finance: Calculating interest, compound growth, and loan repayments all rely on algebraic manipulations.
Advanced Concepts and Further Exploration
While this article focused on simplifying expressions with like terms, the principles discussed form a solid foundation for tackling more complex algebraic manipulations. Further exploration could involve:
-
Expressions with Unlike Terms: Learning to group and simplify expressions containing unlike terms.
-
Expanding Brackets: Applying the distributive property to expand expressions containing brackets.
-
Factorization: Identifying common factors and rewriting expressions in factored form.
-
Solving Equations: Using simplification techniques to solve for unknown variables in equations.
-
Polynomials: Working with expressions involving multiple terms with different powers of the variables.
Conclusion:
Simplifying the algebraic expression 8x - 9x, resulting in -x, is a fundamental skill in algebra. Understanding the concept of like terms, coefficients, and the distributive property is crucial for mastering more advanced algebraic concepts. This seemingly simple operation forms the bedrock for solving more complex equations and understanding mathematical relationships across various disciplines. Through consistent practice and a grasp of the underlying principles, mastering algebraic simplification will significantly enhance your problem-solving abilities and open doors to more advanced mathematical concepts.
Latest Posts
Latest Posts
-
La Senora Castillo El Centro
Sep 22, 2025
-
4 X 3 4x 12
Sep 22, 2025
-
Centripetal Force Examples Human Geography
Sep 22, 2025
-
What Is Sin 30 Degrees
Sep 22, 2025
-
120 89 What Is The Pulse
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Simplify 8x - 9x Completely . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.