Simplify 9 X 7 X
gasmanvison
Sep 11, 2025 · 4 min read
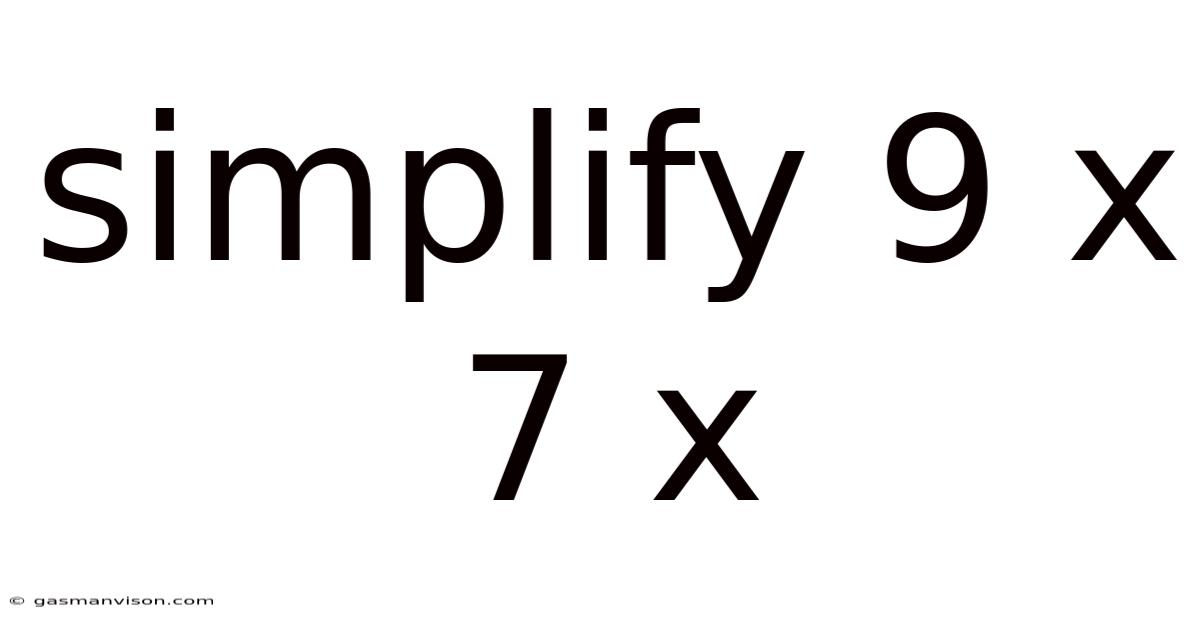
Table of Contents
Simplify 9 x 7 x: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple calculation of 9 x 7 x, delving beyond the immediate answer to uncover the underlying mathematical principles, practical applications, and broader connections within mathematics. While the core calculation is straightforward, understanding its implications opens doors to a deeper appreciation of arithmetic and its role in problem-solving. We'll examine various methods for solving this multiplication problem, explore the properties of multiplication, and discuss how this foundational concept extends to more complex mathematical operations and real-world scenarios.
What is 9 x 7? The Basics
The expression "9 x 7 x" is incomplete; it requires a third number to complete the multiplication. Assuming the missing component is a variable or another number, let's consider the core multiplication: 9 x 7. This represents nine groups of seven, or seven groups of nine. The fundamental operation involves repeated addition: adding seven nine times (7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7) or adding nine seven times (9 + 9 + 9 + 9 + 9 + 9 + 9). Both approaches yield the same result: 63.
Methods for Solving 9 x 7
Several methods can be used to calculate 9 x 7 efficiently:
-
Traditional Multiplication: The standard method involves setting up the numbers vertically and performing the multiplication step-by-step.
-
Distributive Property: We can break down 9 into 10 - 1, utilizing the distributive property: 7 x (10 - 1) = (7 x 10) - (7 x 1) = 70 - 7 = 63. This method is useful for mental calculations, particularly with numbers close to multiples of 10.
-
Multiplication Table: Familiarity with the multiplication table provides an immediate answer. This method relies on memorization, which is a fundamental skill in mathematics.
-
Visual Representation: Imagine a 9 x 7 grid. Counting the total number of squares within the grid gives the product, providing a visual understanding of multiplication.
Properties of Multiplication Relevant to 9 x 7
Understanding the properties of multiplication enhances our ability to solve mathematical problems efficiently. These properties apply to the calculation of 9 x 7 and many other multiplication problems:
-
Commutative Property: The order of the numbers doesn't affect the result. 9 x 7 is equal to 7 x 9. This property allows flexibility in approaching multiplication problems.
-
Associative Property: When multiplying three or more numbers, the grouping of the numbers doesn't affect the product. For example, (9 x 7) x 2 = 9 x (7 x 2). This is crucial when dealing with more complex expressions.
-
Identity Property: Multiplying any number by 1 results in the same number. This is a foundational property in multiplication.
-
Zero Property: Multiplying any number by 0 results in 0. This is another essential property to remember.
-
Distributive Property (as mentioned above): This property allows us to distribute multiplication over addition or subtraction, simplifying calculations.
Extending the Concept: 9 x 7 x 'x'
Let's now consider the complete expression 9 x 7 x 'x', where 'x' represents an unknown value. This introduces the concept of algebraic expressions. To simplify this expression, we first multiply 9 and 7: 63x. This highlights the link between arithmetic and algebra: arithmetic operations form the foundation for algebraic manipulation.
If 'x' were assigned a numerical value, the expression would simplify to a single numerical answer. For instance:
- If x = 2: 9 x 7 x 2 = 126
- If x = 5: 9 x 7 x 5 = 315
- If x = 10: 9 x 7 x 10 = 630
Real-World Applications of Multiplication
The seemingly simple calculation of 9 x 7 has widespread applications in various real-world scenarios:
-
Shopping: Calculating the total cost of multiple items. For example, buying 7 items at $9 each.
-
Construction: Determining the number of bricks needed for a wall or the amount of material for a project.
-
Cooking: Scaling up or down recipes based on the number of servings. Multiplying ingredient quantities.
-
Finance: Calculating interest, discounts, or profits. Multiplication is fundamental in various financial calculations.
-
Data Analysis: Performing calculations on datasets, such as finding averages or totals.
-
Geometry: Calculating areas and volumes. Finding the area of a rectangle with sides 9 and 7 units.
Connecting to More Advanced Mathematics
The concept of multiplication extends far beyond basic arithmetic:
-
Algebra: Multiplication is a fundamental operation in algebra, used to solve equations and manipulate algebraic expressions.
-
Calculus: Multiplication forms the basis of many calculus operations, including differentiation and integration.
-
Linear Algebra: Matrix multiplication is a crucial operation in linear algebra, used in various applications such as computer graphics and machine learning.
-
Number Theory: Multiplication plays a critical role in number theory, the study of the properties of numbers.
Conclusion: Beyond the Simple Calculation
The seemingly trivial calculation of 9 x 7 x, when explored comprehensively, reveals a wealth of mathematical connections and practical applications. Understanding the underlying principles of multiplication, its various properties, and its connections to more advanced mathematical concepts allows for a deeper appreciation of its significance. Mastering this foundational operation is crucial for success in various fields, emphasizing the importance of building a strong mathematical foundation. From everyday tasks like shopping to complex scientific calculations, multiplication is an indispensable tool, highlighting the power and versatility of this seemingly simple arithmetic operation. This exploration of 9 x 7 x serves as a reminder that even the most basic mathematical concepts hold immense value and potential for growth and understanding.
Latest Posts
Latest Posts
-
What Times What Equals 81
Sep 11, 2025
-
Knowledge Drill 6 3 True False Activity
Sep 11, 2025
-
Ever After A Cinderella Story
Sep 11, 2025
-
Electron Geometry Of Co3 2
Sep 11, 2025
-
Electron Dot Diagram For Oxygen
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Simplify 9 X 7 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.