Square Root Of 2x Squared
gasmanvison
Sep 10, 2025 · 5 min read
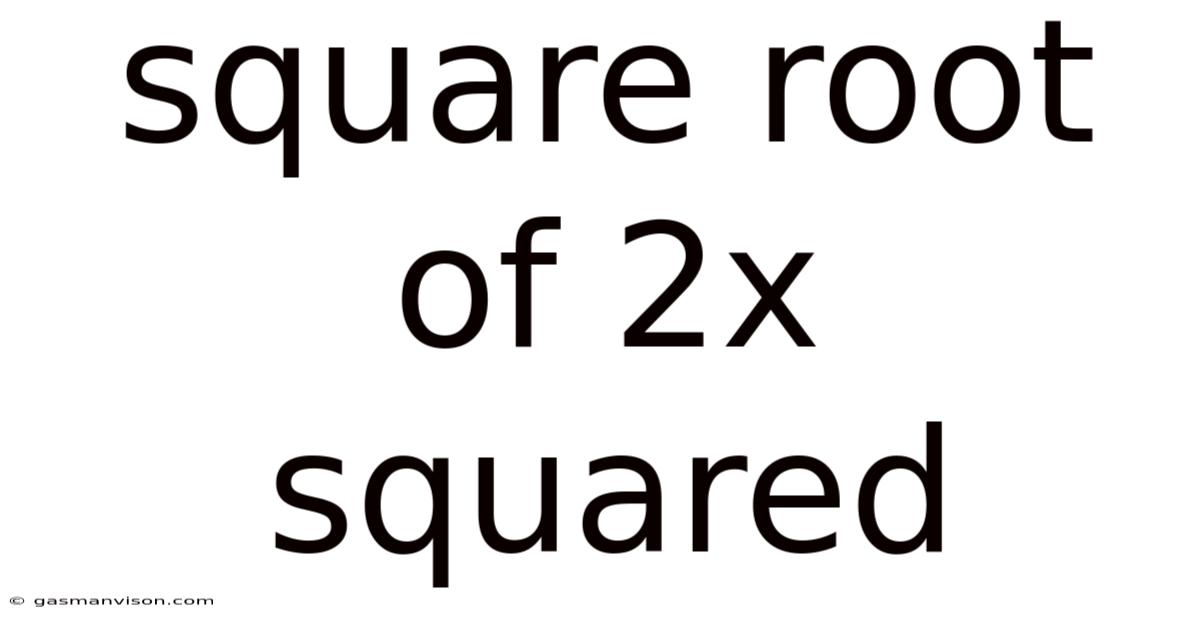
Table of Contents
Unveiling the Mysteries of √(2x²): A Deep Dive into Square Roots and Quadratic Functions
The seemingly simple expression √(2x²) presents a surprisingly rich landscape for exploration, encompassing fundamental concepts in algebra, calculus, and even touches upon more advanced mathematical areas. This comprehensive article will delve into the intricacies of this expression, examining its simplification, graphical representation, applications, and the potential pitfalls in its interpretation. Understanding √(2x²) requires a solid grasp of square roots, quadratic functions, and the crucial concept of absolute value. This article aims to provide that understanding.
What is √(2x²)? A Breakdown of the Expression
At its core, √(2x²) represents the principal square root of the quadratic expression 2x². The principal square root is always the non-negative square root. This immediately introduces a crucial distinction: while x² is always non-negative (for real values of x), √(2x²) requires careful consideration due to the presence of the square root.
We can simplify this expression using the properties of square roots:
√(2x²) = √(2) * √(x²)
Now, we encounter the key point: √(x²) is not simply x. It's the absolute value of x, denoted as |x|. This is because the square root function always returns a non-negative value. Therefore, the correct simplified form of √(2x²) is:
√(2x²) = |x|√2
This seemingly small detail—the absolute value—is crucial for accurately representing the function and avoiding errors in calculations and interpretations. Ignoring the absolute value leads to an incomplete and potentially incorrect understanding of the function's behavior.
Graphical Representation and Domain/Range
Understanding the behavior of √(2x²) is best achieved through its graphical representation. Because the simplified expression involves the absolute value of x, the graph will be symmetric about the y-axis (an even function). The graph will start at the origin (0,0) and extend infinitely in the positive y-direction.
-
Domain: The domain of √(2x²) consists of all real numbers, as any real number can be squared and then have its square root taken (considering only real numbers). Therefore, the domain is (-∞, ∞).
-
Range: Since the absolute value of x is always non-negative, and √2 is a positive constant, the range is limited to non-negative values. The range is [0, ∞).
The graph will resemble a parabola's upper half, but with a steeper incline due to the √2 multiplier. The absolute value ensures that the negative x-values mirror the positive x-values, creating a V-shaped graph.
Derivatives and Calculus Considerations
Applying calculus concepts to √(2x²) provides further insights into its behavior. Let's examine its derivative:
To find the derivative, we'll consider two cases due to the absolute value:
-
Case 1: x ≥ 0 In this case, |x| = x, so the function is √2 * x. The derivative is simply √2.
-
Case 2: x < 0 In this case, |x| = -x, so the function is -√2 * x. The derivative is -√2.
This indicates that the derivative is a piecewise function:
d/dx (√(2x²)) = √2 if x ≥ 0 -√2 if x < 0
This piecewise derivative reflects the sharp change in slope at x = 0, a characteristic feature of functions involving absolute values. The function is not differentiable at x = 0 itself.
Applications and Real-World Context
The square root of 2x² finds applications in various fields, though often implicitly. Here are some examples:
-
Physics: Calculations involving distance, velocity, and acceleration sometimes involve expressions similar to √(2x²), especially when dealing with magnitudes (ignoring direction). For instance, the magnitude of a two-dimensional vector might involve this kind of expression.
-
Geometry: Determining the length of the diagonal of a rectangle with sides x and x√2 would involve this expression. The Pythagorean theorem is directly relevant here.
-
Engineering: Various engineering problems involving magnitudes and distances could utilize this expression. For example, the distance between two points in a Cartesian coordinate system might lead to calculations similar to this.
-
Computer Graphics: The manipulation and transformation of 2D points in computer graphics often involve mathematical operations that include functions similar to √(2x²).
It’s important to note that these applications often involve the magnitude (absolute value) of a quantity, which is why the accurate simplification including the absolute value is critical.
Potential Pitfalls and Common Mistakes
One of the most common mistakes when dealing with √(2x²) is neglecting the absolute value. Simply writing √(2x²) = x√2 is incorrect and leads to inaccurate results, particularly when considering negative values of x. Remember, the square root function always returns a non-negative value.
Another potential issue lies in interpreting the derivative. The non-differentiability at x=0 needs to be understood correctly. While the function is continuous at x=0, its slope changes abruptly, representing a sharp point or cusp in the graph.
Advanced Considerations and Extensions
The exploration of √(2x²) can be extended to more advanced mathematical concepts:
-
Complex Numbers: If we allow for complex values of x, the simplification changes significantly. The square root of a negative number introduces imaginary units (i), and the expression becomes more intricate.
-
Multivariable Calculus: Extending to higher dimensions involves functions of multiple variables, leading to partial derivatives and more complex analysis.
Conclusion: A Comprehensive Understanding
Understanding the expression √(2x²) requires a careful and detailed analysis. The absolute value is crucial for accurate simplification and interpretation. The graphical representation highlights the function's behavior, while calculus provides tools to analyze its rate of change. The seemingly simple expression opens doors to deeper understanding of core mathematical principles and their applications in various fields. Careful attention to detail, particularly regarding the absolute value, is vital for avoiding common mistakes and ensuring a correct interpretation. This comprehensive exploration hopefully clarifies the subtleties of √(2x²) and enhances your mathematical understanding. Remember, grasping these fundamental concepts provides a solid foundation for tackling more advanced mathematical challenges.
Latest Posts
Latest Posts
-
Y 3 2y 7 76
Sep 10, 2025
-
Does The R Group Change
Sep 10, 2025
-
What Process Produces Carbon Dioxide
Sep 10, 2025
-
Express 0 8918 As A Fraction
Sep 10, 2025
-
Relationship Building At Work Can
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 2x Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.