Y 3 2y 7 76
gasmanvison
Sep 10, 2025 · 5 min read
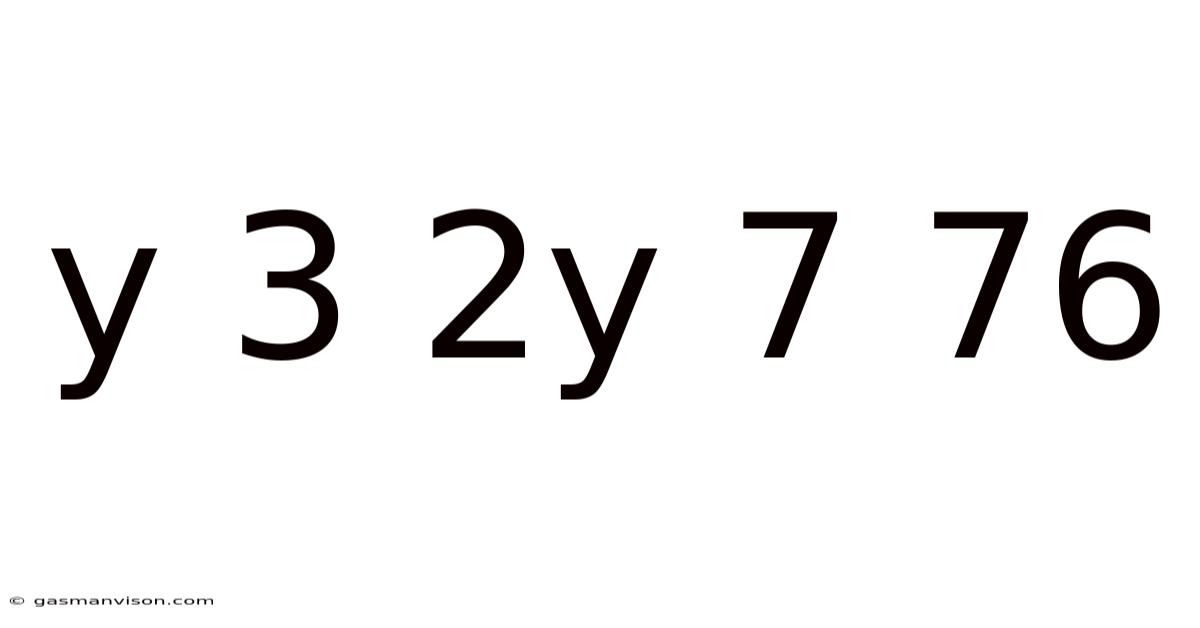
Table of Contents
Decoding the Enigma: Exploring the Mathematical Possibilities of "y 3 2y 7 76"
This seemingly simple string of characters, "y 3 2y 7 76," presents a fascinating challenge. At first glance, it appears to be an incomplete or poorly formatted mathematical equation. However, a deeper dive reveals a potential treasure trove of mathematical exploration, encompassing various interpretations and solutions depending on the assumptions made. This article will analyze multiple interpretations of this cryptic expression, exploring potential solutions and highlighting the importance of clear mathematical notation. We will delve into algebra, potentially touch upon calculus depending on interpretation, and stress the crucial role of context in mathematical problem-solving.
Understanding the Ambiguity: The Importance of Context
The primary hurdle in deciphering "y 3 2y 7 76" lies in its ambiguity. The lack of standard mathematical operators (+, -, ×, ÷, =, etc.) and parentheses leaves room for multiple interpretations. This ambiguity underscores the critical importance of precise mathematical notation. Without clear symbols, multiple valid interpretations are possible, each leading to a different solution.
Let's explore some potential interpretations and solve them systematically.
Interpretation 1: A Simple Algebraic Equation
We can interpret "y 3 2y 7 76" as a simplified algebraic equation, assuming the spaces represent addition or subtraction. This approach generates several possibilities:
- Possibility A: y + 3 + 2y + 7 = 76
This interpretation leads to a straightforward linear equation. Combining like terms, we get:
3y + 10 = 76
Subtracting 10 from both sides:
3y = 66
Dividing by 3:
y = 22
- Possibility B: y + 3 - 2y + 7 = 76
This interpretation results in:
-y + 10 = 76
Subtracting 10 from both sides:
-y = 66
Multiplying by -1:
y = -66
- Possibility C: y + 3 + 2y - 7 = 76
This leads to:
3y - 4 = 76
Adding 4 to both sides:
3y = 80
Dividing by 3:
y ≈ 26.67
- Possibility D: y - 3 + 2y - 7 = 76 And other similar variations.
These examples demonstrate the impact of seemingly minor changes in the assumed operators. Each variation yields a distinct solution for y, highlighting the necessity of explicit mathematical notation.
Interpretation 2: A Sequence or Pattern
Another interpretation involves considering "y 3 2y 7 76" as a numerical sequence or pattern. This approach requires identifying a relationship between the numbers. Without more information or context, identifying a definitive pattern is challenging. However, we can explore some potential patterns:
-
Arithmetic Progression: If we assume an arithmetic progression, we could look for a common difference between consecutive terms. However, the presence of "y" complicates this significantly, as it's an unknown variable.
-
Geometric Progression: Similarly, assuming a geometric progression (where each term is multiplied by a constant to get the next term) yields no immediate solutions without further constraints.
-
Recursive Sequence: It's conceivable that "y 3 2y 7 76" represents a recursive sequence, where each term depends on the previous one(s). However, without defining the recursive rule, this remains speculative. Further information would be needed to define a recurrence relation.
This interpretation opens up a broader, more abstract mathematical problem, emphasizing the need for a clearly defined mathematical structure to solve it.
Interpretation 3: Encoded Message or Cipher
Taking a more creative approach, we could consider "y 3 2y 7 76" as a form of encoded message or a simple cipher. This interpretation would involve decoding the string of characters using known cipher techniques.
-
Substitution Cipher: We could hypothesize that the letters and numbers represent substituted characters, with "y" potentially standing for a specific number or symbol. Without a key, this remains purely speculative.
-
Caesar Cipher: A Caesar cipher involves shifting each letter or number by a certain amount. This method is easily broken given enough ciphertext, but without the key or more data, it's implausible to decode "y 3 2y 7 76".
Without additional context or clues, this interpretation is highly speculative and unlikely to yield a definitive answer.
Interpretation 4: Functional Notation (Advanced)
If we were to make some considerable assumptions, we could interpret "y 3 2y 7 76" as a compressed notation for a function. However, this would require making substantial assumptions about the meaning of the spaces and the arrangement.
For example, one might hypothetically interpret this as multiple functions being applied sequentially:
-
f(y) = 3
-
g(x) = 2x + 7
-
h(z) = z - 76
Then, one might attempt to combine these functions. However, such an interpretation is highly speculative and needs a substantial degree of contextual information to be remotely meaningful. The lack of clearly defined operational symbols makes this approach impractical without making too many assumptions.
The Crucial Role of Clear Notation in Mathematics
The ambiguity of "y 3 2y 7 76" underscores the critical importance of precise mathematical notation. The lack of clear symbols leads to multiple possible interpretations, highlighting the need for accuracy and consistency in expressing mathematical relationships. Ambiguous notation can lead to confusion, misinterpretations, and ultimately, incorrect solutions.
Conclusion: The Value of Defined Problems
This exercise of interpreting "y 3 2y 7 76" serves as a valuable lesson in mathematical problem-solving. It demonstrates that clear, unambiguous notation is essential for effective communication and accurate results. The multiplicity of potential solutions based on different interpretations highlights the importance of well-defined problems and the need for context in mathematical reasoning. While we explored several potential avenues, none lead to a single, definitive solution without further clarifying information. The ambiguity inherent in the original expression showcases the crucial role of precise communication within the realm of mathematics. The primary takeaway is not the finding of a solution, but the understanding that precise notation is fundamentally crucial for any mathematical problem to be clearly understood and solved.
Latest Posts
Latest Posts
-
Dietary Recalls Include Information About
Sep 10, 2025
-
Before Heavily Soiled Condiment Pans
Sep 10, 2025
-
What Is 2 Of 180
Sep 10, 2025
-
What Is 25 Of 520
Sep 10, 2025
-
Assuming You Tested An Organism
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Y 3 2y 7 76 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.