What Is 40 Of 220
gasmanvison
Sep 05, 2025 · 5 min read
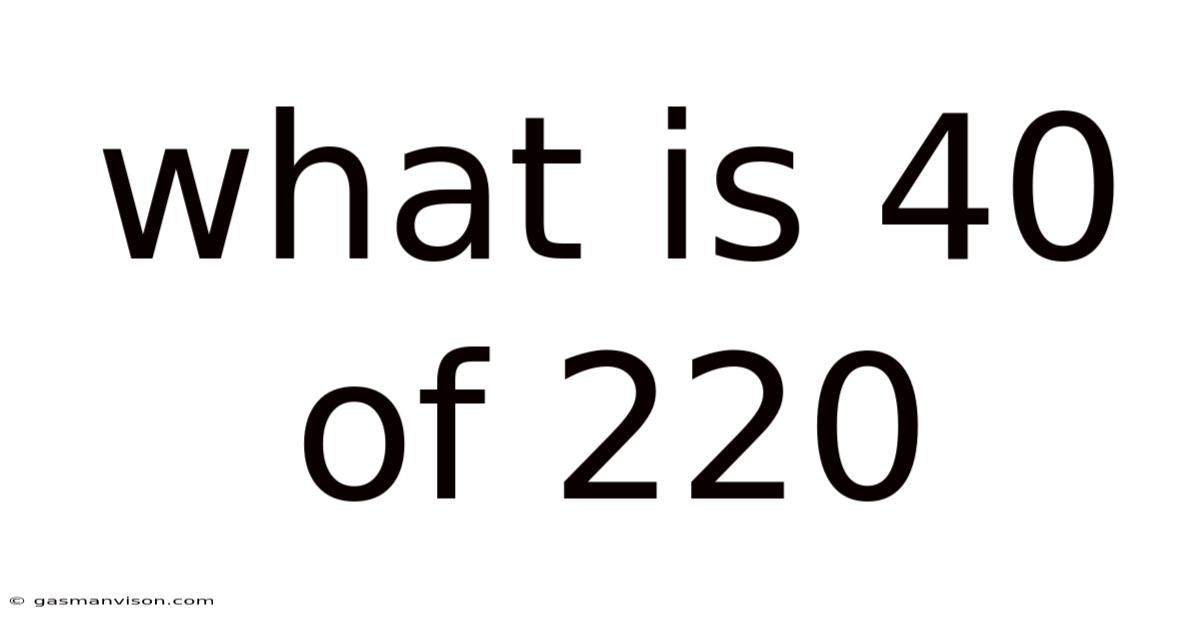
Table of Contents
What is 40% of 220? A Deep Dive into Percentages and Their Applications
This article will comprehensively explore the calculation of 40% of 220, delving beyond the simple answer to explain the underlying principles of percentages, their practical applications, and how to perform similar calculations efficiently. Understanding percentages is crucial in various aspects of life, from finance and budgeting to data analysis and scientific research. This guide will equip you with the knowledge and skills to confidently tackle percentage problems.
Meta Description: Learn how to calculate 40% of 220 and master percentage calculations. This comprehensive guide explains the process, explores practical applications, and provides tips for solving similar problems.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (from the Latin per centum). Therefore, 40% can be represented as 40/100 or 0.40 (as a decimal). This representation forms the basis of all percentage calculations.
Calculating 40% of 220: The Basic Approach
The most straightforward way to calculate 40% of 220 is to convert the percentage to a decimal and then multiply it by the number:
- Convert the percentage to a decimal: 40% = 40/100 = 0.40
- Multiply the decimal by the number: 0.40 * 220 = 88
Therefore, 40% of 220 is 88.
Alternative Methods for Calculating Percentages
While the above method is the most common, several alternative approaches can be used depending on the specific problem and your preferred calculation method.
-
Using Fractions: Expressing the percentage as a fraction simplifies the calculation in some cases. 40% can be expressed as 2/5. Therefore, calculating 40% of 220 becomes (2/5) * 220 = 440/5 = 88.
-
Proportions: Set up a proportion to solve for the unknown value. Let 'x' represent 40% of 220:
40/100 = x/220
Cross-multiply and solve for x:
100x = 40 * 220 100x = 8800 x = 8800/100 x = 88
-
Using a Calculator: Most calculators have a percentage function (%) that simplifies the process. Simply enter 220, press the multiplication key, then enter 40 and the percentage key. The calculator will automatically perform the calculation and display the result as 88.
Practical Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous real-world scenarios. Here are a few examples:
-
Finance and Budgeting: Calculating discounts, interest rates, tax amounts, and profit margins all involve percentage calculations. For example, understanding the interest rate on a loan or the discount on a sale price requires proficiency in percentage calculations. Calculating your savings rate or determining the impact of inflation on your investments also depends on percentages.
-
Data Analysis and Statistics: Percentages are widely used to represent data in charts, graphs, and tables. They allow for easy comparison of proportions within datasets, such as comparing market shares of competing companies, success rates of different treatments, or voter preferences in an election. Understanding percentage change, percentage points, and relative frequency are crucial for accurate data interpretation.
-
Sales and Marketing: Calculating sales targets, commission rates, conversion rates, and customer acquisition costs all require a strong understanding of percentages. Marketing professionals use percentage calculations to measure the effectiveness of various campaigns and strategies. For instance, understanding click-through rates, bounce rates, and conversion rates relies heavily on percentage calculations.
-
Science and Engineering: Percentages are used extensively in scientific and engineering applications, such as expressing concentrations of solutions, measuring efficiency of processes, and calculating error margins. For example, calculating the percentage purity of a substance, the efficiency of a machine, or the percentage error in an experiment uses percentage calculations.
-
Everyday Life: From calculating tips in restaurants to understanding sales tax, percentages are incorporated into many aspects of our daily lives. Determining the percentage increase in fuel prices or understanding the percentage of ingredients in a recipe are everyday applications of percentages.
Advanced Percentage Calculations: Percentage Increase and Decrease
Beyond the basic calculation of a percentage of a number, understanding percentage increase and decrease is crucial for various applications.
-
Percentage Increase: This calculation determines the percentage by which a value has increased. The formula is:
[(New Value - Original Value) / Original Value] * 100%
-
Percentage Decrease: This calculation determines the percentage by which a value has decreased. The formula is:
[(Original Value - New Value) / Original Value] * 100%
For example, if a product's price increased from $100 to $120, the percentage increase is:
[(120 - 100) / 100] * 100% = 20%
Troubleshooting Common Percentage Calculation Mistakes
Several common mistakes can occur when working with percentages. Here are some to watch out for:
-
Incorrect Decimal Conversion: Ensure you correctly convert the percentage to a decimal before multiplying. A common mistake is to use the percentage directly in the calculation without converting it.
-
Misinterpreting Percentage Points: Percentage points represent the arithmetic difference between two percentages, not the percentage change. For example, an increase from 10% to 20% is a 10-percentage-point increase, but a 100% percentage increase.
-
Confusing Percentage Increase and Decrease: Make sure you use the correct formula depending on whether you're calculating an increase or a decrease. Using the wrong formula will result in an incorrect answer.
-
Rounding Errors: Be mindful of rounding errors, especially when dealing with multiple calculations involving percentages. Rounding off intermediate results can lead to significant inaccuracies in the final answer.
Improving Your Percentage Calculation Skills
To improve your percentage calculation skills, practice regularly. Work through various examples, using different methods to gain a deeper understanding. You can find numerous practice problems online or in textbooks. Focus on understanding the underlying principles rather than simply memorizing formulas. Mastering percentages will significantly improve your analytical and problem-solving abilities across multiple disciplines.
Conclusion: Beyond 40% of 220
While the initial question, "What is 40% of 220?" has a simple answer (88), this article has expanded upon the concept, exploring the fundamental principles of percentages, their diverse applications, and common calculation methods. Understanding percentages is a valuable skill applicable to numerous fields and aspects of daily life. By mastering these concepts, you'll be better equipped to tackle complex problems and make informed decisions in various situations. Remember to practice regularly and utilize the various approaches to solidify your understanding of this crucial mathematical concept. The ability to confidently perform percentage calculations translates to a deeper understanding of data, financial matters, and a wide range of other essential areas.
Latest Posts
Latest Posts
-
30 000 Ft To Miles
Sep 07, 2025
-
Mystery In Wexford Answer Key
Sep 07, 2025
-
How Many Lbs Is 15kg
Sep 07, 2025
-
How Much Is 500 Kilos
Sep 07, 2025
-
3 3 4 X 2 4 5
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about What Is 40 Of 220 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.