What Is 40 Of 35
gasmanvison
Sep 09, 2025 · 5 min read
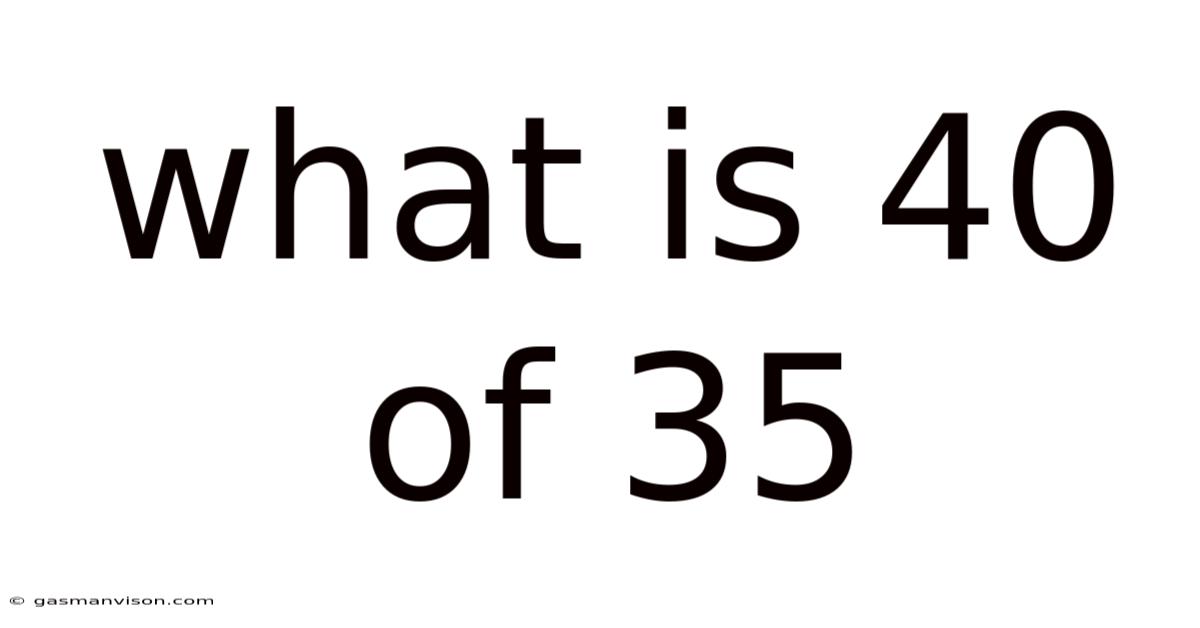
Table of Contents
What is 40% of 35? A Deep Dive into Percentage Calculations and Their Applications
What is 40% of 35? At first glance, this seems like a simple question with a straightforward answer. However, understanding how to calculate percentages, and more importantly, the underlying concepts, opens doors to a vast world of applications across various fields, from finance and statistics to everyday life. This article will not only provide the answer but also explore the different methods of calculating percentages, their real-world applications, and common pitfalls to avoid.
Meta Description: Learn how to calculate 40% of 35 and master percentage calculations. This comprehensive guide covers various methods, real-world applications, and common mistakes to avoid, helping you confidently tackle percentage problems.
Understanding Percentages: The Basics
A percentage is a fraction or a ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred." The symbol "%" represents this fraction. For example, 40% can be written as 40/100 or 0.40. This fundamental understanding is crucial for tackling any percentage calculation.
Method 1: Using the Formula
The most straightforward method to calculate 40% of 35 is using the basic percentage formula:
Percentage × Number = Result
In this case:
40% × 35 = ?
First, convert the percentage to a decimal: 40% = 0.40
Then, multiply the decimal by the number:
0.40 × 35 = 14
Therefore, 40% of 35 is 14.
Method 2: Using Fractions
Percentages can also be expressed as fractions. 40% is equivalent to 40/100, which can be simplified to 2/5. We can then use this fraction to calculate 40% of 35:
(2/5) × 35 = (2 × 35) / 5 = 70 / 5 = 14
This method demonstrates the interchangeable nature of percentages, decimals, and fractions, highlighting the versatility of percentage calculations.
Method 3: Using Proportions
Proportions offer another effective method for solving percentage problems. We can set up a proportion:
40/100 = x/35
Where 'x' represents the unknown value (40% of 35). To solve for x, we cross-multiply:
40 × 35 = 100 × x
1400 = 100x
x = 1400 / 100 = 14
Again, we arrive at the answer: 40% of 35 is 14.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is a crucial skill with widespread applications in various aspects of life:
-
Finance: Calculating interest rates, discounts, taxes, profits, and losses all rely heavily on percentage calculations. Understanding percentage change is essential for analyzing investment performance and understanding market fluctuations. For instance, calculating the discount on a sale item, determining the interest earned on a savings account, or understanding tax deductions all involve percentages.
-
Statistics: Percentages are fundamental to expressing data in a concise and understandable manner. Data analysis, surveys, and research frequently use percentages to present findings effectively. Understanding concepts like percentage increase/decrease, relative frequency, and percentiles are crucial in interpreting statistical data. For example, understanding polling data, interpreting election results, or assessing demographic changes relies on percentage analysis.
-
Everyday Life: Calculating tips in restaurants, figuring out sale prices, determining the percentage of ingredients in a recipe, or understanding nutritional information on food labels all involve percentage calculations. These everyday applications highlight the practical importance of mastering percentage calculations.
-
Science and Engineering: Percentages are commonly used in scientific measurements, expressing error rates, and representing concentrations in chemical solutions.
Common Mistakes to Avoid When Calculating Percentages
While percentage calculations seem straightforward, several common mistakes can lead to inaccurate results:
-
Incorrect Decimal Conversion: Failing to convert the percentage to a decimal before multiplication is a frequent error. Remember, 40% is 0.40, not 40.
-
Misunderstanding the "of": The word "of" in percentage problems always indicates multiplication. "40% of 35" means 40% * 35.
-
Incorrect Proportion Setup: When using proportions, ensuring the correct values are placed in the corresponding positions is vital. A misplaced number can lead to an incorrect answer.
-
Rounding Errors: While rounding might be necessary for simplicity, be mindful of potential errors. Rounding too early in the calculation can significantly affect the final result. It's always best to round only at the final step.
Advanced Percentage Calculations
Beyond the basics, several more complex percentage calculations exist:
-
Percentage Change: This measures the relative change between two values. The formula is: [(New Value - Old Value) / Old Value] × 100%. Understanding percentage change is critical for analyzing trends and growth rates.
-
Percentage Points: A percentage point represents the absolute difference between two percentages. For example, an increase from 10% to 15% is a 5 percentage point increase, not a 50% increase.
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. The formula is more complex but crucial for understanding long-term investments and loan repayments.
Practical Exercises
To solidify your understanding, try these exercises:
- Calculate 25% of 80.
- What percentage of 60 is 15?
- If a price increases from $50 to $60, what is the percentage increase?
- A shirt is on sale for 30% off its original price of $45. What is the sale price?
Conclusion
Calculating 40% of 35, while seemingly simple, unlocks a deeper understanding of percentages and their extensive applications. Mastering percentage calculations equips you with a valuable skill applicable in various fields and everyday situations. By understanding the different methods and avoiding common pitfalls, you can confidently tackle percentage problems and analyze data more effectively. Remember to practice regularly and explore the more advanced concepts to further enhance your proficiency. The ability to accurately calculate and interpret percentages will undoubtedly benefit you both professionally and personally.
Latest Posts
Latest Posts
-
Stackwalk2 Could Not Be Located
Sep 09, 2025
-
Ounces In A Half Pound
Sep 09, 2025
-
Reversible Lanes Are Used During
Sep 09, 2025
-
17 12 As A Mixed Number
Sep 09, 2025
-
What Best Describes Hydrostatic Pressure
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 40 Of 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.