What Is Equivalent To 4/8
gasmanvison
Sep 25, 2025 · 6 min read
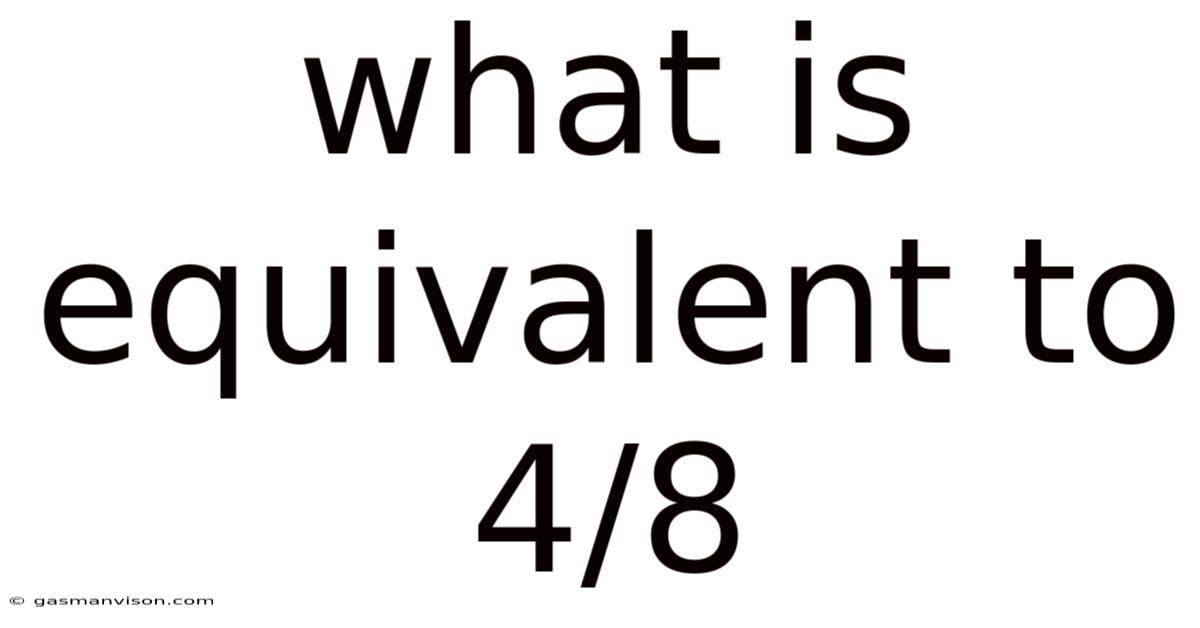
Table of Contents
What is Equivalent to 4/8? Unpacking Fractions and Equivalent Fractions
This seemingly simple question, "What is equivalent to 4/8?", opens a door to a fundamental concept in mathematics: equivalent fractions. Understanding equivalent fractions is crucial not only for mastering basic arithmetic but also for tackling more advanced mathematical concepts like algebra, geometry, and calculus. This article will delve deep into the meaning of equivalent fractions, explore various methods for finding them, and highlight their practical applications. We'll go beyond simply stating the answer and explore the underlying principles, making this a comprehensive guide for anyone wanting to solidify their understanding of fractions.
Meta Description: Discover the world of equivalent fractions! Learn what is equivalent to 4/8 and explore multiple methods to find equivalent fractions. This in-depth guide covers simplifying fractions, visual representations, and real-world applications. Master this essential mathematical concept today.
Understanding Fractions: A Quick Refresher
Before diving into equivalent fractions, let's briefly revisit the concept of a fraction itself. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For example, in the fraction 4/8, the denominator 8 signifies that the whole is divided into 8 equal parts, and the numerator 4 indicates that we are considering 4 of those parts.
What is Equivalent to 4/8? The Simple Answer
The simplest equivalent fraction to 4/8 is 1/2. This is because both the numerator (4) and the denominator (8) can be divided by their greatest common divisor (GCD), which is 4. Dividing both the numerator and the denominator by 4 simplifies the fraction to its lowest terms: 4 ÷ 4 = 1 and 8 ÷ 4 = 2.
Methods for Finding Equivalent Fractions
There are several ways to find equivalent fractions. Let's explore the most common methods:
1. Simplifying Fractions (Reducing to Lowest Terms):
This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder. For example, to simplify 4/8:
- Find the GCD of 4 and 8, which is 4.
- Divide both the numerator and denominator by 4: 4 ÷ 4 = 1 and 8 ÷ 4 = 2.
- The simplified fraction is 1/2.
This method is particularly useful for expressing fractions in their simplest form, making them easier to understand and compare.
2. Multiplying the Numerator and Denominator by the Same Number:
This is a fundamental principle of equivalent fractions: multiplying both the numerator and the denominator by the same non-zero number results in an equivalent fraction. For example, to find equivalent fractions to 1/2:
- Multiply both the numerator and the denominator by 2: (1 × 2) / (2 × 2) = 2/4
- Multiply both the numerator and the denominator by 3: (1 × 3) / (2 × 3) = 3/6
- Multiply both the numerator and the denominator by 4: (1 × 4) / (2 × 4) = 4/8
This method allows you to generate an infinite number of equivalent fractions for any given fraction.
3. Dividing the Numerator and Denominator by the Same Number:
This is the reverse of the previous method. If both the numerator and denominator share a common factor, dividing both by that factor will result in an equivalent fraction. This is essentially simplifying the fraction. For example, starting with 12/18:
- Both 12 and 18 are divisible by 2: 12 ÷ 2 = 6 and 18 ÷ 2 = 9, giving 6/9.
- Both 6 and 9 are divisible by 3: 6 ÷ 3 = 2 and 9 ÷ 3 = 3, giving 2/3.
- Therefore, 12/18, 6/9, and 2/3 are all equivalent fractions.
4. Visual Representations:
Visual aids such as pie charts, bar models, or number lines can effectively demonstrate the concept of equivalent fractions. Imagine a pie cut into 8 slices. Shading 4 of those slices represents 4/8. Now, imagine grouping those 4 shaded slices into two larger sections. Each section represents half the pie, visually demonstrating that 4/8 is equivalent to 1/2. This visual approach helps solidify understanding, especially for visual learners.
Practical Applications of Equivalent Fractions
Equivalent fractions are not just an abstract mathematical concept; they have numerous real-world applications:
-
Cooking and Baking: Recipes often require fractions of ingredients. Understanding equivalent fractions allows you to adjust recipes based on the available quantities. For instance, if a recipe calls for 1/2 cup of sugar, you can use an equivalent fraction like 2/4 or 4/8 cup if needed.
-
Measurement and Units: Converting between different units of measurement often involves working with equivalent fractions. For example, converting inches to feet or centimeters to meters requires understanding how these units relate to each other through fractional equivalents.
-
Sharing and Division: Dividing objects or resources fairly often requires the use of fractions and their equivalents. If you need to share a pizza among 8 people, each person gets 1/8. If only 4 people are sharing, each person gets 4/8 or 1/2 of the pizza.
-
Geometry and Area: Calculating areas of shapes often involves fractions. Understanding equivalent fractions helps simplify calculations and express the results in the simplest form.
-
Probability and Statistics: Probability is often expressed as a fraction. Equivalent fractions can be used to represent the same probability in different forms, making it easier to compare probabilities.
Beyond 4/8: Working with Other Fractions
The principles discussed above apply to all fractions. To find equivalent fractions for any given fraction, follow the methods described:
- Simplify: Find the GCD of the numerator and denominator and divide both by it.
- Multiply: Multiply both the numerator and the denominator by the same non-zero number.
- Divide: Divide both the numerator and the denominator by the same common factor.
Conclusion: Mastering Equivalent Fractions
Understanding equivalent fractions is a cornerstone of mathematical proficiency. This article has explored the meaning of equivalent fractions, multiple methods for finding them, and their practical applications in various contexts. By mastering this fundamental concept, you build a solid foundation for tackling more complex mathematical challenges and applying mathematical reasoning to real-world scenarios. Remember, the ability to simplify and manipulate fractions is essential for success in many areas of life, far beyond the classroom. From baking a cake to understanding statistics, the knowledge of equivalent fractions is a powerful tool. So, the next time you encounter a fraction, remember the power of simplification and the myriad ways equivalent fractions can help you solve problems efficiently and accurately.
Latest Posts
Latest Posts
-
What Does Inversely Proportional Mean
Sep 25, 2025
-
3 7 8 As A Decimal
Sep 25, 2025
-
In The Bedroom In Spanish
Sep 25, 2025
-
Graph Y 3x 2 1
Sep 25, 2025
-
How Many Ounces Are 500ml
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about What Is Equivalent To 4/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.