What Plus What Equals 24
gasmanvison
Sep 10, 2025 · 5 min read
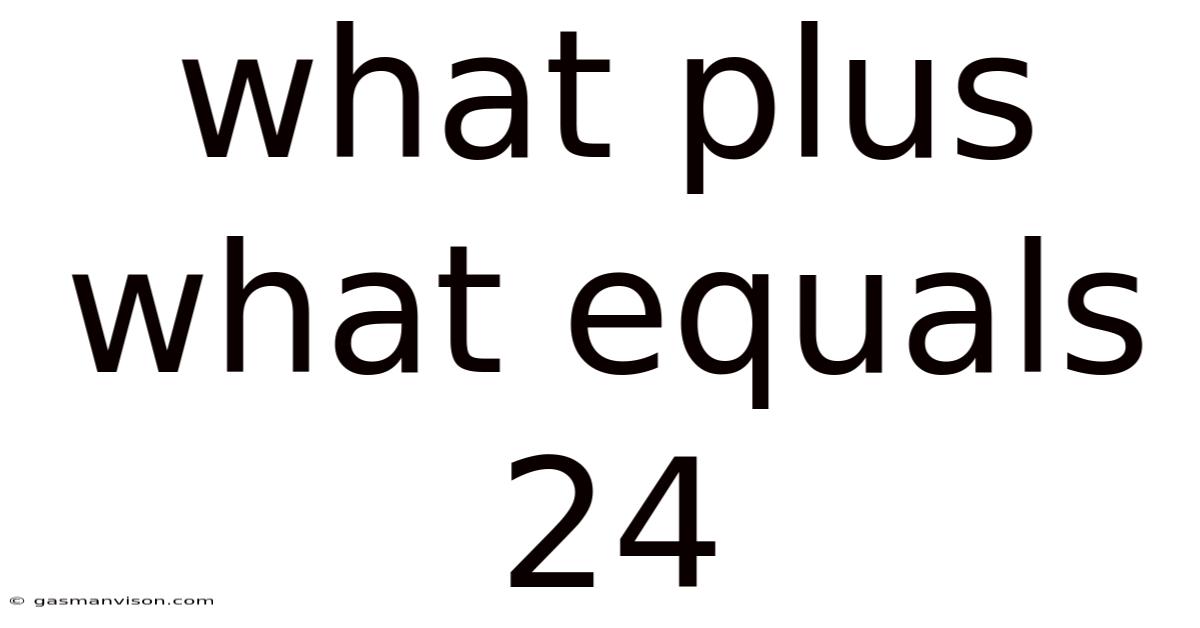
Table of Contents
What Plus What Equals 24? Exploring the Possibilities and Applications of Addition
This seemingly simple question, "What plus what equals 24?", opens a door to a vast world of mathematical possibilities. While the immediate answer might seem obvious – 12 + 12, for example – exploring this equation unveils a rich tapestry of numerical relationships, problem-solving strategies, and practical applications across various fields. This article delves deep into the numerous solutions, explores different approaches to finding them, and discusses the significance of this seemingly basic arithmetic problem.
Meta Description: Discover the multiple solutions to the equation "What plus what equals 24?" This article explores various mathematical approaches, discusses practical applications, and reveals the surprising depth hidden within this simple addition problem.
The equation "x + y = 24" has infinitely many solutions if we consider all real numbers. However, if we restrict ourselves to whole numbers, positive integers, or even specific sets of numbers, the number of solutions dramatically decreases, making the problem more interesting and challenging. Let's explore these different scenarios:
Solutions Using Whole Numbers
The most straightforward approach involves using whole numbers. Here are a few examples:
- 12 + 12 = 24: This is the most obvious and symmetrical solution.
- 11 + 13 = 24: A slightly different combination, showcasing the flexibility of the equation.
- 10 + 14 = 24: Continuing the pattern, we see multiple possibilities emerging.
- 1 + 23 = 24: Highlighting the range of possible solutions.
- 2 + 22 = 24
- 3 + 21 = 24
- 4 + 20 = 24
- 5 + 19 = 24
- 6 + 18 = 24
- 7 + 17 = 24
- 8 + 16 = 24
- 9 + 15 = 24
These examples demonstrate that there are twelve pairs of whole numbers that add up to 24. This showcases the diverse range of solutions available within the confines of whole numbers.
Exploring Solutions with Negative Numbers
Expanding our scope to include negative numbers opens up an even wider range of possibilities. For instance:
- 0 + 24 = 24: Introducing zero as a valid addend.
- 100 + (-76) = 24: Demonstrating the use of negative numbers.
- (-5) + 29 = 24: Further illustrating the flexibility with negative integers.
- (-100) + 124 = 24: Showing that large negative numbers can also be part of the solution.
The inclusion of negative numbers dramatically increases the number of potential solutions, making the seemingly simple equation infinitely more complex. This highlights the importance of specifying the domain (the set of numbers allowed) when solving such problems.
Fractions and Decimals: Expanding the Possibilities
If we permit fractions and decimals, the possibilities become truly limitless. Consider these examples:
- 12.5 + 11.5 = 24: Introducing decimal numbers into the equation.
- 23.75 + 0.25 = 24: Showing the use of decimals with different magnitudes.
- 1/2 + 47/2 = 24: Illustrating the use of fractions.
- 10 + 14 = 24
The introduction of fractions and decimals expands the solution set to an infinite number of combinations. Any number 'x' can be paired with '24-x' to achieve the desired sum. This underscores the importance of clearly defining the constraints of the problem.
Practical Applications: Where Does This Equation Matter?
While seemingly basic, the concept of finding two numbers that sum to a specific value has far-reaching practical applications in various fields:
- Inventory Management: Imagine a warehouse manager needs to allocate 24 units of a product across two different storage locations. This equation helps determine the various possible distribution scenarios.
- Financial Accounting: Balancing budgets, allocating resources, or calculating profit margins often involve finding two values that add up to a predetermined total.
- Engineering and Physics: Many engineering and physics problems involve solving equations where the sum of two variables equals a constant. For example, calculating forces in equilibrium or determining the components of vectors.
- Game Development: In video games, particularly those with resource management or puzzle elements, determining combinations of resources or points that add up to a specific target value is crucial.
- Data Analysis: In statistical analysis and data science, finding pairs of data points that sum to a particular value can be essential for pattern recognition and trend identification.
These are just a few examples. The principle of finding two numbers that add up to a specific value is a fundamental concept woven into the fabric of numerous fields, showcasing its broad applicability.
Problem-Solving Strategies: Beyond Simple Addition
Solving "What plus what equals 24?" isn't just about finding a single answer; it's about understanding different approaches to problem-solving:
- Trial and Error: The simplest approach, starting with educated guesses and refining them until the solution is found. This method is particularly useful when dealing with smaller numbers.
- Algebraic Approach: Using the equation x + y = 24, one can solve for one variable in terms of the other (e.g., y = 24 - x), allowing for systematic exploration of possible solutions.
- Systematic Listing: Creating a table or list of pairs of numbers, systematically checking their sum until the desired result (24) is achieved.
- Computational Methods: For large datasets or more complex problems, computational methods and algorithms can efficiently find solutions.
Each method offers a unique perspective and is valuable in different contexts. The choice of method depends on the complexity of the problem, the available resources, and the desired level of precision.
Expanding the Question: Variations and Extensions
The simplicity of "What plus what equals 24?" allows for interesting variations and extensions:
- What plus what plus what equals 24? This introduces a new dimension of complexity, increasing the number of possible solutions.
- What three numbers add up to 24? Similar to the above, but allowing for numbers to be the same.
- Find three consecutive numbers that add up to 24. This introduces a constraint, limiting the possible solutions.
These variations highlight the versatility of the fundamental concept of addition and its adaptability to increasingly intricate problem-solving scenarios.
Conclusion: The Enduring Significance of a Simple Equation
The seemingly simple question, "What plus what equals 24?", reveals a surprising depth and breadth of mathematical concepts and practical applications. From the straightforward solutions using whole numbers to the limitless possibilities introduced by negative numbers, fractions, and decimals, this equation serves as a powerful illustration of the richness and versatility of mathematics. Its applications span various fields, and exploring different problem-solving strategies underscores the importance of critical thinking and adaptability. Ultimately, this simple addition problem demonstrates the profound power of fundamental mathematical principles in addressing complex real-world challenges. The enduring significance of this equation lies not just in its answers, but in the journey of exploration and discovery it prompts.
Latest Posts
Latest Posts
-
What Rule Describes The Translation
Sep 10, 2025
-
Medicare Integrity Contractors Medtrainer Answers
Sep 10, 2025
-
Y 3 2y 7 76
Sep 10, 2025
-
Does The R Group Change
Sep 10, 2025
-
What Process Produces Carbon Dioxide
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about What Plus What Equals 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.