Whats 20 Percent Of 40
gasmanvison
Sep 14, 2025 · 5 min read
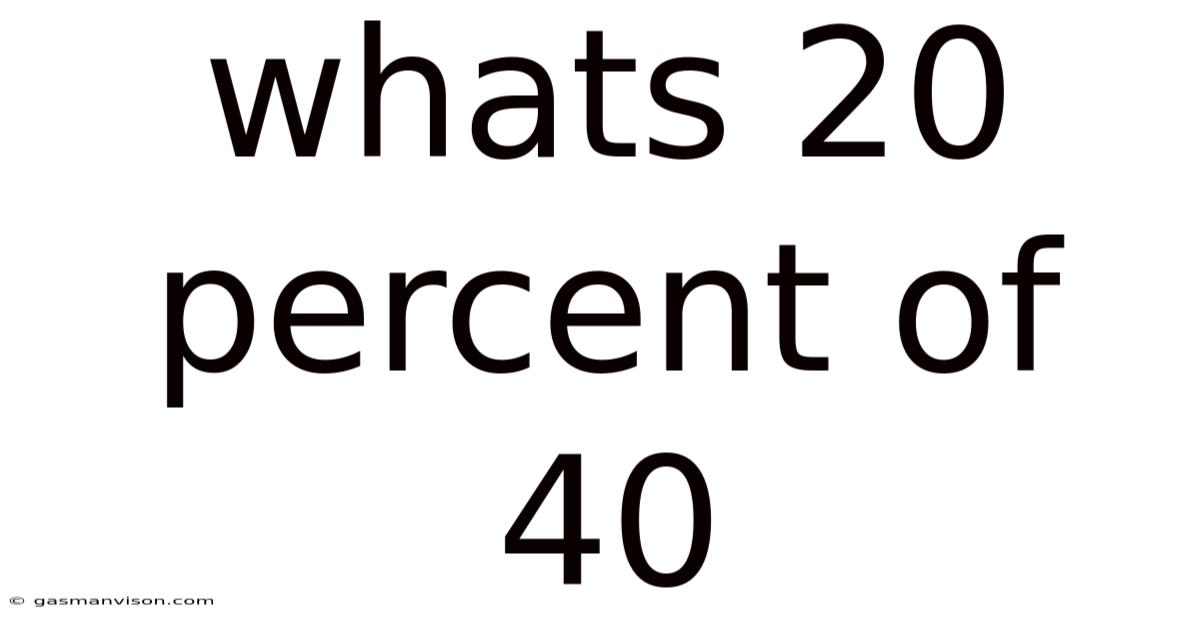
Table of Contents
What's 20 Percent of 40? A Deep Dive into Percentages and Their Applications
Finding 20 percent of 40 might seem like a simple calculation, but understanding the underlying principles unlocks a world of practical applications in various fields. This seemingly basic question opens doors to understanding percentages, a crucial concept in mathematics and everyday life. This comprehensive guide will not only answer the question but also explore the different methods for calculating percentages, their real-world uses, and some advanced percentage-related problems.
Meta Description: Learn how to calculate 20% of 40 and delve into the world of percentages. Discover various methods, real-world applications, and advanced percentage problems. Master this fundamental concept for everyday life and beyond.
Understanding Percentages: The Fundamentals
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" comes from the Latin "per centum," meaning "out of a hundred." Therefore, 20% signifies 20 parts out of 100 equal parts. This fundamental understanding is crucial for grasping percentage calculations.
Method 1: The Fraction Method
This is arguably the most intuitive approach. We can rewrite 20% as a fraction: 20/100. To find 20% of 40, we simply multiply the fraction by 40:
(20/100) * 40 = 8
Therefore, 20% of 40 is 8.
Method 2: The Decimal Method
Another common method involves converting the percentage to a decimal. To convert a percentage to a decimal, divide it by 100. So, 20% becomes 0.20 (or simply 0.2). Then, multiply this decimal by 40:
0.2 * 40 = 8
Again, we arrive at the answer: 8.
Method 3: Using Proportions
This method is particularly useful for understanding the relationship between percentages and their corresponding values. We can set up a proportion:
20/100 = x/40
Here, 'x' represents the value we're trying to find (20% of 40). To solve for 'x', we cross-multiply:
20 * 40 = 100 * x 800 = 100x x = 800/100 x = 8
This confirms our answer: 20% of 40 is 8.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in many real-world scenarios. Here are a few examples:
-
Sales and Discounts: Calculating discounts on sale items. For instance, a 20% discount on a $40 item results in a savings of $8.
-
Taxes: Determining the amount of sales tax or income tax. If the sales tax is 6%, calculating the tax on a purchase involves percentage calculations.
-
Tips and Gratuities: Calculating the appropriate tip at a restaurant. A 15% tip on a $40 meal involves a percentage calculation.
-
Finance and Investments: Calculating interest earned on savings accounts or investments. Understanding compound interest requires a strong grasp of percentages.
-
Statistics and Data Analysis: Percentages are fundamental in representing and interpreting data. For example, representing survey results or market share often involves percentages.
-
Science and Engineering: Percentages are used in many scientific calculations, such as calculating error margins or concentrations.
-
Cooking and Baking: Scaling recipes up or down involves understanding and adjusting percentages of ingredients.
-
Everyday Budgeting: Tracking expenses and income often involves calculating percentages to understand spending habits and savings goals.
Advanced Percentage Problems
Let's explore some more complex scenarios involving percentages:
Scenario 1: Finding the Original Price After a Discount
A shirt is on sale for $24 after a 20% discount. What was the original price?
This problem requires working backward. If $24 represents 80% (100% - 20%) of the original price, we can set up a proportion:
80/100 = 24/x
Solving for x:
80x = 2400 x = 30
The original price of the shirt was $30.
Scenario 2: Calculating Percentage Increase or Decrease
A stock price increased from $20 to $25. What is the percentage increase?
First, calculate the difference: $25 - $20 = $5
Then, divide the difference by the original price and multiply by 100%:
(5/20) * 100% = 25%
The stock price increased by 25%.
Scenario 3: Compound Interest
If you invest $1000 at an annual interest rate of 5% compounded annually, how much will you have after 2 years?
Year 1: $1000 * 0.05 = $50 interest. Total: $1050 Year 2: $1050 * 0.05 = $52.50 interest. Total: $1102.50
After 2 years, you will have $1102.50. Note that compound interest involves calculating percentages repeatedly.
Tips for Mastering Percentage Calculations
-
Practice Regularly: The more you practice, the more comfortable you'll become with percentage calculations. Start with simple problems and gradually move to more complex ones.
-
Use Multiple Methods: Try different methods to solve the same problem. This helps to solidify your understanding and identify the most efficient approach for you.
-
Understand the Underlying Concepts: Focus on understanding the core principles of percentages rather than just memorizing formulas.
-
Utilize Online Resources: Numerous online calculators and tutorials can help you practice and refine your skills.
-
Real-World Application: Apply your knowledge to real-life scenarios, like calculating discounts or tips. This will reinforce your understanding and make the concepts more relevant.
Conclusion
While the question "What's 20 percent of 40?" might seem simple, its answer unlocks a vast understanding of percentages and their crucial role in various aspects of life. Mastering percentage calculations equips you with essential skills applicable to finance, sales, statistics, and more. By employing different methods and practicing regularly, you can confidently navigate the world of percentages and confidently tackle even the most complex percentage-related problems. Remember that understanding the fundamental principles is key to mastering this important mathematical concept. From everyday budgeting to advanced financial analysis, a strong grasp of percentages is invaluable.
Latest Posts
Latest Posts
-
Ci Includes Only Offensive Activities
Sep 14, 2025
-
Any Incidents Or Unusual Activity
Sep 14, 2025
-
Chris Kyle Longest Sniper Shot
Sep 14, 2025
-
What Is 30 Off 60
Sep 14, 2025
-
Graph Y 1 2f X
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Whats 20 Percent Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.