Whats 20 Percent Of 75
gasmanvison
Sep 24, 2025 · 4 min read
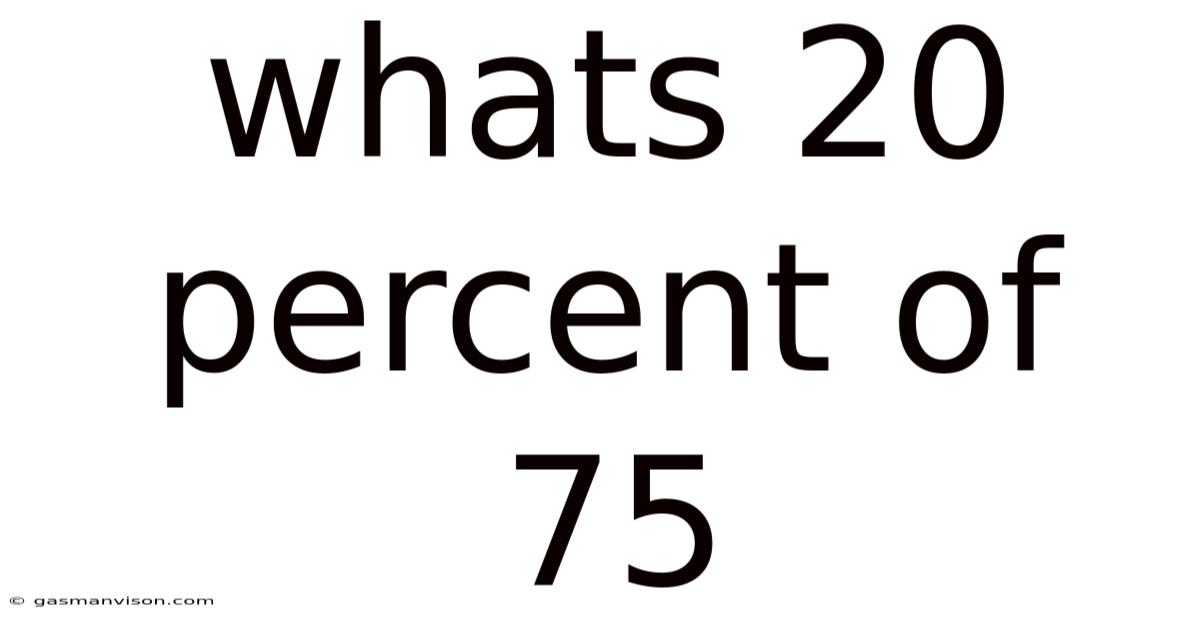
Table of Contents
What's 20 Percent of 75? A Deep Dive into Percentage Calculations and Their Applications
Finding 20 percent of 75 might seem like a simple calculation, but understanding the underlying principles opens doors to a wide range of applications in various fields. This article will not only answer the question directly but also explore the different methods for calculating percentages, their practical uses, and how to apply these concepts to more complex scenarios. We'll delve into the mathematical foundations, offer practical examples, and even touch upon using technology to perform these calculations efficiently.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 20 percent (20%) means 20 out of 100, or 20/100, which simplifies to 1/5. This fundamental understanding is crucial for tackling percentage problems.
Calculating 20% of 75: Three Methods
There are several ways to calculate 20% of 75. Let's explore three common methods:
1. The Decimal Method:
This is arguably the most straightforward method. We convert the percentage to a decimal by dividing it by 100. 20% becomes 0.20 (or simply 0.2). Then, we multiply this decimal by the number we're finding the percentage of:
75 * 0.2 = 15
Therefore, 20% of 75 is $\boxed{15}$.
2. The Fraction Method:
As mentioned earlier, 20% is equivalent to the fraction 1/5. We can calculate 20% of 75 by multiplying 75 by 1/5:
75 * (1/5) = 75/5 = 15
Again, the result is $\boxed{15}$.
3. The Proportion Method:
This method uses proportions to solve for the unknown value. We set up a proportion:
20/100 = x/75
Where 'x' represents 20% of 75. To solve for x, we cross-multiply:
20 * 75 = 100 * x
1500 = 100x
x = 1500/100 = 15
Once more, we arrive at the answer: $\boxed{15}$.
Real-World Applications of Percentage Calculations
Understanding percentages is essential in numerous everyday situations, including:
-
Finance: Calculating interest on loans, savings accounts, and investments. Understanding discounts and sales tax. Analyzing financial statements and budgets.
-
Shopping: Determining the sale price of an item after a percentage discount. Comparing prices and finding the best deals. Calculating tips in restaurants.
-
Science: Expressing experimental results as percentages. Analyzing data and drawing conclusions from percentages. Calculating concentrations of solutions.
-
Statistics: Analyzing survey results and representing data using percentages. Understanding statistical significance and probability.
-
Business: Calculating profit margins, market share, and growth rates. Analyzing sales data and making informed business decisions.
Beyond the Basics: More Complex Percentage Problems
While calculating 20% of 75 is relatively simple, let's consider more complex scenarios where understanding percentages becomes crucial:
1. Finding the Original Value:
Let's say you bought an item on sale for $60 after a 25% discount. To find the original price, you can set up the equation:
Original Price * (1 - 0.25) = $60
Original Price * 0.75 = $60
Original Price = $60 / 0.75 = $80
The original price was $\boxed{$80}$.
2. Calculating Percentage Increase or Decrease:
Suppose a company's revenue increased from $50,000 to $60,000. To calculate the percentage increase:
Percentage Increase = [(New Value - Old Value) / Old Value] * 100
Percentage Increase = [($60,000 - $50,000) / $50,000] * 100 = 20%
The revenue increased by $\boxed{20%}$.
3. Compound Percentage Changes:
Imagine investing $1000 with a 10% annual interest rate compounded annually for 3 years. The calculation isn't simply 30% (10% * 3). Compound interest means you earn interest on the interest. The calculation would be:
Year 1: $1000 * 1.10 = $1100 Year 2: $1100 * 1.10 = $1210 Year 3: $1210 * 1.10 = $1331
After 3 years, you'd have $\boxed{$1331}$.
Using Technology for Percentage Calculations
While manual calculations are valuable for understanding the underlying principles, technology can significantly simplify and speed up the process, particularly for more complex calculations. Spreadsheets (like Microsoft Excel or Google Sheets) and online calculators are readily available and can handle various percentage calculations efficiently. Many calculators have dedicated percentage buttons, simplifying the process.
Conclusion:
Understanding how to calculate percentages is a fundamental skill with broad applications across numerous disciplines. While the seemingly simple problem of finding 20% of 75 serves as a great starting point, mastering percentage calculations empowers you to tackle more complex problems in finance, business, science, and everyday life. By understanding the different methods and their applications, you can confidently navigate the world of percentages and make informed decisions based on quantitative data. Remember to leverage technology to streamline your calculations when dealing with complex scenarios, allowing you to focus on the interpretation and application of the results.
Latest Posts
Latest Posts
-
Abiotic Factors In The Taiga
Sep 24, 2025
-
What Is 64 Of 350
Sep 24, 2025
-
5 Divided By 1 3
Sep 24, 2025
-
How Old Is George Washington
Sep 24, 2025
-
Much Ado About Nothing Summary
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Whats 20 Percent Of 75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.