Whats 30 Percent Of 300
gasmanvison
Sep 12, 2025 · 5 min read
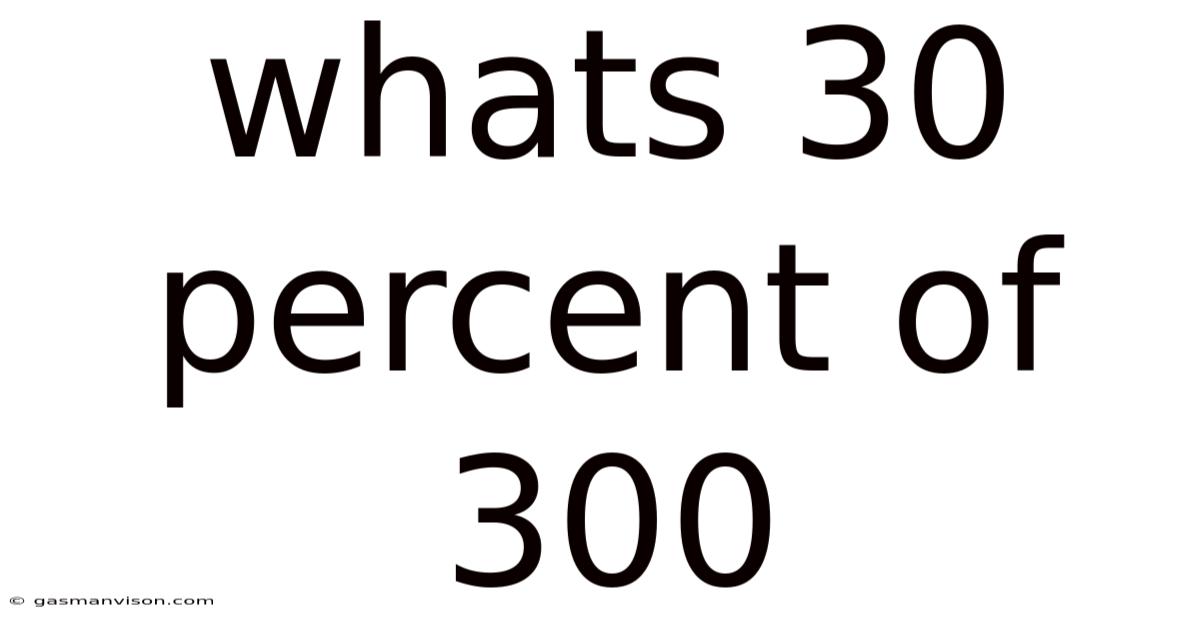
Table of Contents
What's 30 Percent of 300? A Deep Dive into Percentages and Their Applications
Finding 30 percent of 300 might seem like a simple calculation, but understanding the underlying principles of percentages opens doors to a wide range of applications in everyday life, from budgeting and finance to sales and statistics. This article will not only answer the question – what's 30 percent of 300? – but also explore the broader concepts of percentage calculations, their real-world uses, and advanced techniques for solving more complex percentage problems. This comprehensive guide will equip you with the knowledge to confidently tackle any percentage-related challenge.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." Understanding this basic definition is crucial for mastering percentage calculations. To find a percentage of a number, we essentially translate the percentage into a decimal or fraction and then multiply it by the number.
For instance, 30% can be expressed as:
- A fraction: 30/100 (which simplifies to 3/10)
- A decimal: 0.30 (or simply 0.3)
Therefore, finding 30% of 300 involves multiplying 300 by either 30/100 or 0.3.
Calculating 30% of 300: The Simple Approach
The most straightforward method to calculate 30% of 300 is to convert the percentage to a decimal and multiply:
300 * 0.3 = 90
Therefore, 30% of 300 is 90.
Alternative Calculation Methods: Expanding Your Toolkit
While the decimal method is efficient, exploring alternative approaches enhances your understanding and provides flexibility for different problem types.
- Using Fractions: We can also use the fractional representation of 30%, which is 30/100. This simplifies to 3/10. So, the calculation becomes:
(3/10) * 300 = 90
This method is particularly useful when dealing with simpler fractions.
- Finding 10% and Scaling: A helpful strategy, especially for mental calculations, is to find 10% of the number first and then scale it up. 10% of 300 is 30. Since 30% is three times 10%, we simply multiply 30 by 3:
30 * 3 = 90
This method is highly effective for quick estimations and calculations without a calculator.
Real-World Applications of Percentage Calculations
Understanding percentage calculations extends far beyond simple mathematical exercises. They are indispensable tools in numerous real-world scenarios:
-
Finance and Budgeting: Calculating interest rates, discounts, taxes, profit margins, and investment returns all heavily rely on percentage calculations. For instance, understanding the interest rate on a loan or the discount percentage on a sale item is crucial for informed financial decisions. Calculating your monthly budget allocation based on percentages of your income is also essential for responsible financial planning.
-
Sales and Marketing: Percentage calculations are fundamental to determining sales targets, analyzing market share, and measuring the effectiveness of marketing campaigns. Tracking conversion rates (percentage of visitors who make a purchase), calculating customer retention rates, and analyzing sales growth all involve percentages.
-
Data Analysis and Statistics: Percentages are essential for presenting and interpreting data. Expressing data as percentages helps to standardize and compare different datasets, making it easier to identify trends and draw conclusions. Understanding statistical measures like percentages, ratios and proportions, is crucial for interpreting information across various fields including healthcare, education, and research.
-
Everyday Life: We encounter percentages daily. Sales discounts, tips in restaurants, tax rates, and even nutritional information on food labels are all expressed as percentages. A strong grasp of percentage calculations allows for better informed purchasing decisions and a deeper understanding of the numerical world around us.
Tackling More Complex Percentage Problems: Advanced Techniques
While finding 30% of 300 is straightforward, let's explore how to handle more complex percentage problems:
- Finding the Original Number: If you know the percentage and the resulting value, you can work backward to find the original number. For example, if 25% of a number is 50, you would solve it as follows:
50 / 0.25 = 200 (The original number was 200)
- Calculating Percentage Increase or Decrease: Determining percentage changes is common in many applications. For example, if a price increases from $100 to $120, the percentage increase is calculated as:
((120 - 100) / 100) * 100% = 20%
Similarly, a decrease can be calculated using the same formula, resulting in a negative percentage value.
-
Working with Multiple Percentages: Sometimes, you need to work with multiple percentages consecutively. For example, if you receive a 10% discount followed by a 5% additional discount, the final price isn't simply 15% off. You need to apply each discount sequentially.
-
Solving for an Unknown Percentage: Suppose you know the original number and the resulting number after a percentage change, and you want to find the percentage change. You would need to set up an equation and solve for the unknown percentage.
Utilizing Technology for Percentage Calculations
While mastering manual calculation methods is crucial for understanding the underlying principles, technology can simplify complex percentage calculations. Spreadsheets (like Microsoft Excel or Google Sheets) and calculators offer built-in functions to calculate percentages efficiently. Learning to utilize these tools can significantly increase your speed and accuracy in solving percentage problems, especially those involving large datasets or intricate calculations.
Conclusion: Mastering Percentages for a Numerically Literate World
Understanding percentage calculations is a fundamental skill with widespread applicability. While finding 30% of 300 provides a simple starting point, delving into the underlying principles and exploring various calculation methods empowers you to tackle more complex problems confidently. Whether managing finances, analyzing data, or making everyday decisions, a strong grasp of percentages is essential for navigating the numerical world effectively. This article serves as a foundational guide, providing not only the answer to the initial question but also a comprehensive overview of percentage calculations and their diverse applications, equipping you with the tools to become more numerically literate and confident in tackling percentage-related challenges.
Latest Posts
Latest Posts
-
4 Ft 3 In Inches
Sep 12, 2025
-
What Is 75 Of 27
Sep 12, 2025
-
How Many Ml Is 16oz
Sep 12, 2025
-
Ms Florina Buys A Bag
Sep 12, 2025
-
Time Machine Essay Questions Evolution
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Whats 30 Percent Of 300 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.