X 2 6x 5 0
gasmanvison
Sep 15, 2025 · 6 min read
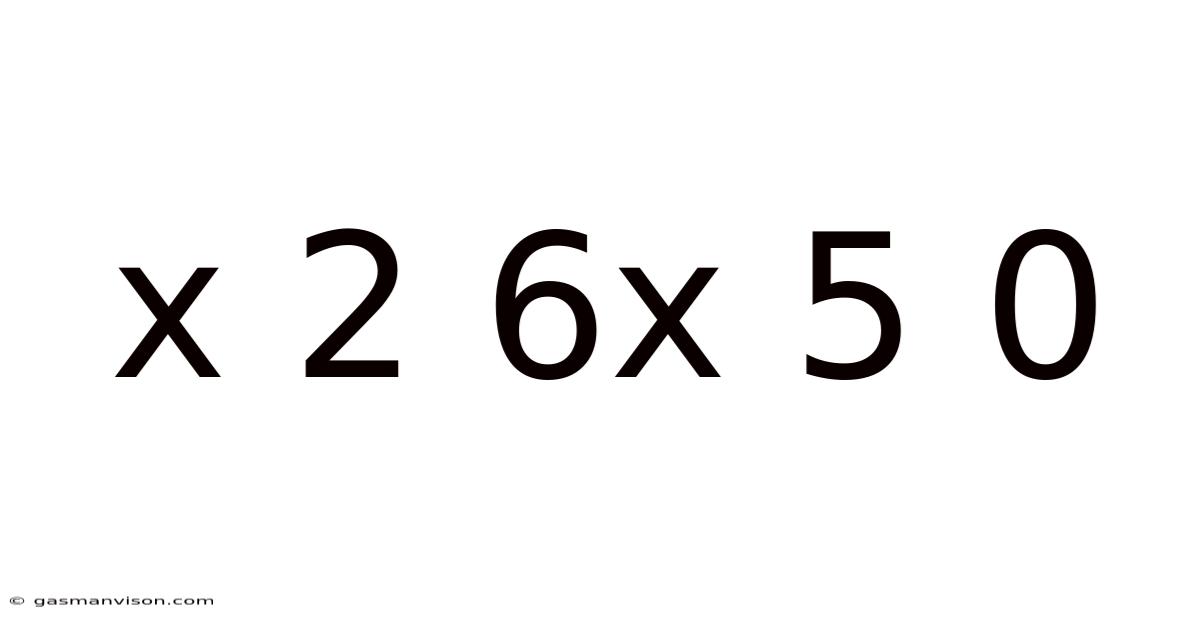
Table of Contents
Decoding x² + 6x + 5 = 0: A Comprehensive Guide to Quadratic Equations
This article delves into the solution of the quadratic equation x² + 6x + 5 = 0, exploring various methods and providing a thorough understanding of the underlying concepts. We'll cover factoring, the quadratic formula, completing the square, and graphical representation, offering a multi-faceted approach to solving this seemingly simple yet fundamentally important equation. This guide is designed for students learning about quadratic equations, as well as anyone looking to refresh their understanding of this core algebraic concept. The equation x² + 6x + 5 = 0 serves as an excellent example to illustrate several key principles within algebra and beyond.
What is a Quadratic Equation?
A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (in this case, x) is 2. It takes the general form ax² + bx + c = 0, where a, b, and c are constants, and a ≠ 0. Our specific example, x² + 6x + 5 = 0, fits this form with a = 1, b = 6, and c = 5. Understanding this general form is crucial for applying various solution methods. These methods are not just limited to solving simple equations; they form the bedrock of more advanced mathematical concepts in fields such as calculus, physics, and engineering. The ability to manipulate and solve quadratic equations efficiently is a valuable skill across numerous disciplines.
Method 1: Factoring
Factoring is often the quickest and most straightforward method for solving quadratic equations, particularly when the factors are easily identifiable. The goal is to rewrite the equation as a product of two binomial expressions. For x² + 6x + 5 = 0, we look for two numbers that add up to 6 (the coefficient of x) and multiply to 5 (the constant term). These numbers are 5 and 1. Therefore, we can factor the equation as follows:
(x + 5)(x + 1) = 0
This equation is true if either (x + 5) = 0 or (x + 1) = 0. Solving for x in each case gives us the two solutions:
x = -5 or x = -1
These are the roots or zeros of the quadratic equation. They represent the x-intercepts of the parabola that would be graphed from this equation. The ability to quickly factor quadratic equations demonstrates a strong understanding of algebraic manipulation and number relationships.
Method 2: The Quadratic Formula
The quadratic formula is a more general approach that works for all quadratic equations, even those that are difficult or impossible to factor easily. The formula is derived from completing the square (explained in the next section) and provides a direct solution for x:
x = [-b ± √(b² - 4ac)] / 2a
Substituting the values from our equation (a = 1, b = 6, c = 5), we get:
x = [-6 ± √(6² - 4 * 1 * 5)] / (2 * 1) x = [-6 ± √(36 - 20)] / 2 x = [-6 ± √16] / 2 x = [-6 ± 4] / 2
This gives us two solutions:
x = (-6 + 4) / 2 = -1 x = (-6 - 4) / 2 = -5
As expected, the quadratic formula yields the same solutions as factoring. The quadratic formula is a powerful tool, ensuring a solution can always be found, regardless of the equation's factorability. Understanding its derivation and application is crucial for mastering quadratic equations. Furthermore, the discriminant (b² - 4ac) within the formula provides valuable information about the nature of the roots (real and distinct, real and equal, or complex).
Method 3: Completing the Square
Completing the square is a technique used to manipulate a quadratic equation into a perfect square trinomial, which can then be easily solved. It's a fundamental algebraic method with applications beyond quadratic equations. The process involves manipulating the equation to create a perfect square on one side. For x² + 6x + 5 = 0:
-
Move the constant term to the right side: x² + 6x = -5
-
Take half of the coefficient of x (6), square it (9), and add it to both sides: x² + 6x + 9 = -5 + 9 x² + 6x + 9 = 4
-
Rewrite the left side as a perfect square: (x + 3)² = 4
-
Take the square root of both sides: x + 3 = ±2
-
Solve for x: x = -3 ± 2
This gives us the same solutions as before:
x = -1 or x = -5
Completing the square not only provides a solution but also helps in understanding the graphical representation of the quadratic equation, which is discussed in the next section. This method highlights the relationship between the equation's coefficients and its vertex.
Graphical Representation
The equation x² + 6x + 5 = 0 represents a parabola. The solutions (-1 and -5) are the x-intercepts, where the parabola crosses the x-axis. The parabola opens upwards because the coefficient of x² (a = 1) is positive. The vertex of the parabola, representing the minimum point, can be found using the formula x = -b/2a. In our case:
x = -6 / (2 * 1) = -3
Substituting x = -3 back into the original equation gives the y-coordinate of the vertex:
y = (-3)² + 6(-3) + 5 = -4
Therefore, the vertex of the parabola is (-3, -4). This graphical representation provides a visual understanding of the solutions and the overall behavior of the quadratic function. The graph vividly demonstrates the relationship between the roots and the parabola's characteristics. Understanding graphical representation enhances the intuitive understanding of quadratic equations beyond mere algebraic manipulation.
Applications of Quadratic Equations
Quadratic equations are not merely abstract mathematical concepts; they have numerous real-world applications across various fields. Some examples include:
- Physics: Calculating projectile motion, determining the trajectory of objects under the influence of gravity.
- Engineering: Designing parabolic antennas, bridges, and arches.
- Economics: Modeling supply and demand curves, optimizing production levels.
- Computer graphics: Creating curves and shapes in computer-aided design (CAD) software.
The ability to solve quadratic equations is fundamental to understanding and modeling these real-world phenomena. The diverse applications highlight the importance of mastering this algebraic skill. The seemingly simple equation x² + 6x + 5 = 0 serves as a foundational example for these more complex applications.
Conclusion
Solving x² + 6x + 5 = 0 through factoring, the quadratic formula, and completing the square showcases different approaches to solving quadratic equations. Each method offers unique insights into the underlying algebraic principles and provides different perspectives on the problem. Understanding these methods, coupled with the graphical representation of the equation, allows for a comprehensive grasp of quadratic equations and their significant role in various fields. This detailed analysis underscores the importance of mastering quadratic equations as a fundamental building block for advanced mathematical concepts and their applications in the real world. The seemingly simple equation serves as a gateway to a deeper understanding of algebra and its pervasive influence across diverse disciplines. By understanding the multiple solution methods and the graphical representation, one gains a comprehensive and holistic understanding of quadratic equations and their broader significance.
Latest Posts
Latest Posts
-
How Much Is 3000 Pennies
Sep 15, 2025
-
Motorists Driving Large Trucks Shoud
Sep 15, 2025
-
16 Oz Is A Lb
Sep 15, 2025
-
What Is 2 5 Equivalent To
Sep 15, 2025
-
90 Confidence Interval Z Score
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about X 2 6x 5 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.