140 Percent As A Fraction
gasmanvison
Sep 13, 2025 · 5 min read
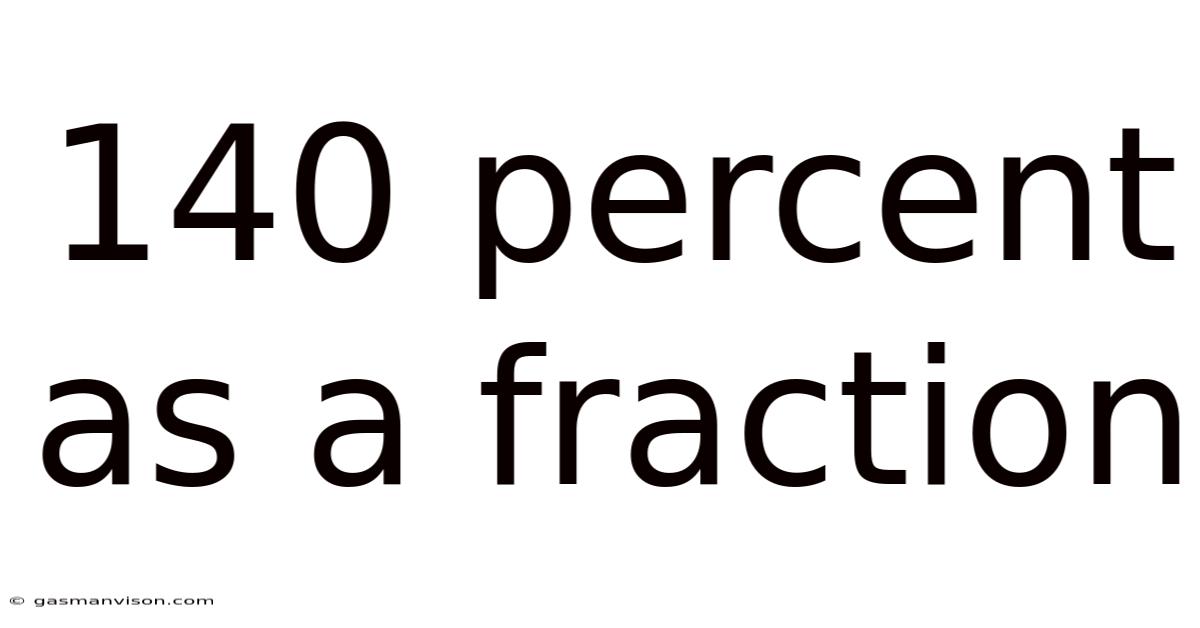
Table of Contents
140 Percent as a Fraction: A Comprehensive Guide
Understanding percentages and their fractional equivalents is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and interest rates to comprehending statistical data and analyzing financial reports. This article delves deep into the conversion of 140 percent into a fraction, exploring the process, its simplification, and various related concepts. We'll also examine practical examples showcasing the utility of this conversion in different scenarios.
What is a Percentage?
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" (from the Latin per centum). So, 140 percent means 140 out of 100, or 140/100. This representation is inherently a fraction.
Converting 140 Percent to a Fraction: The Step-by-Step Process
The conversion of 140 percent to a fraction is straightforward:
-
Write the percentage as a fraction with a denominator of 100: 140% becomes 140/100.
-
Simplify the fraction: Both the numerator (140) and the denominator (100) are divisible by 20. Dividing both by 20, we get:
140 ÷ 20 = 7 100 ÷ 20 = 5
Therefore, the simplified fraction is 7/5.
-
Express as a mixed number (optional): Since the numerator (7) is larger than the denominator (5), we can express the improper fraction as a mixed number. Dividing 7 by 5, we get 1 with a remainder of 2. This means 7/5 is equivalent to 1 2/5.
Therefore, 140 percent as a fraction is 7/5, or 1 2/5.
Understanding Improper Fractions and Mixed Numbers
In the process above, we encountered an improper fraction (7/5) and its equivalent mixed number (1 2/5). Let's clarify these terms:
-
Improper Fraction: An improper fraction is a fraction where the numerator is greater than or equal to the denominator. Examples include 7/5, 9/4, and 11/11.
-
Mixed Number: A mixed number combines a whole number and a proper fraction. It represents a quantity greater than one. Examples include 1 2/5, 2 3/4, and 5 1/2.
Converting between improper fractions and mixed numbers is a crucial skill for working with fractions effectively.
Practical Applications of Converting Percentages to Fractions
The ability to convert percentages to fractions is invaluable in numerous situations:
-
Calculating Increases and Decreases: Suppose a company's profits increase by 140 percent. This means the increase is 7/5 of the original profit. Understanding this fractional representation allows for easier calculations of the new profit amount.
-
Financial Calculations: Interest rates, discounts, and tax calculations often involve percentages. Expressing these percentages as fractions simplifies complex calculations and provides a clearer understanding of the financial implications. For example, a 140% markup on a $10 item would mean adding (7/5) * $10 = $14 to the original price, resulting in a $24 final price.
-
Statistical Analysis: Many statistical measures, such as proportions and ratios, are expressed as fractions or percentages. Converting between these forms allows for easier comparison and interpretation of data. A survey indicating 140% response rate (perhaps due to multiple responses per person) is easily understood as 7/5 the expected response, highlighting an anomaly requiring further investigation.
-
Recipe Scaling: If a recipe calls for 140% of a certain ingredient, converting this to 7/5 allows for easy scaling up or down of the recipe. For example, if the recipe calls for 1 cup of flour, you'd need 7/5 cups, or 1.4 cups of flour.
-
Geometry and Measurement: Problems involving proportions in geometry frequently utilize percentage-to-fraction conversion for accurate calculations.
Further Exploration: Working with Different Percentages
While this article focuses on 140 percent, the method used for conversion applies to any percentage. Let's briefly look at a few examples:
-
50%: 50/100 simplifies to 1/2.
-
25%: 25/100 simplifies to 1/4.
-
125%: 125/100 simplifies to 5/4 or 1 1/4.
-
300%: 300/100 simplifies to 3.
Note that percentages greater than 100% result in improper fractions or whole numbers, representing quantities larger than the original whole.
Beyond the Basics: Decimal Equivalents
Percentages can also be easily converted to decimals. To convert a percentage to a decimal, divide by 100. For example, 140% as a decimal is 1.4. This decimal representation is another way to express the same quantity, and it's often preferred for calculations using calculators or computer software. Understanding the relationships between fractions, decimals, and percentages enhances mathematical flexibility.
Error Handling and Common Mistakes
When working with percentages and fractions, it's essential to be mindful of common mistakes:
-
Incorrect Simplification: Always ensure the fraction is simplified to its lowest terms. Failure to simplify can lead to inaccurate calculations.
-
Misinterpreting Mixed Numbers: Ensure you correctly convert between improper fractions and mixed numbers. Incorrect conversion can lead to flawed results.
-
Confusing Percentage Increase/Decrease: Distinguish between percentage increases and percentage decreases, ensuring you are applying the percentage correctly to the base value.
Conclusion
Converting 140 percent to a fraction, resulting in 7/5 or 1 2/5, is a fundamental mathematical operation with broad applicability across various disciplines. Understanding this conversion, along with the underlying concepts of improper fractions, mixed numbers, and the relationships between percentages, decimals, and fractions, empowers individuals to tackle mathematical problems with greater confidence and accuracy. The ability to seamlessly transition between these different representations unlocks a deeper understanding of mathematical relationships and their practical implications in real-world scenarios. The more you practice these conversions, the more intuitive they will become. Remember to always check your work and ensure your final answer is simplified to its lowest terms.
Latest Posts
Latest Posts
-
A Routine Medication Is Given
Sep 14, 2025
-
Molar Mass Of Ammonium Phosphate
Sep 14, 2025
-
X 3 2x 2 3x
Sep 14, 2025
-
Aquellos Sombreros Son Muy Elegantes
Sep 14, 2025
-
X 2 Y 2 16
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 140 Percent As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.