Y 2 X 1 2
gasmanvison
Sep 13, 2025 · 6 min read
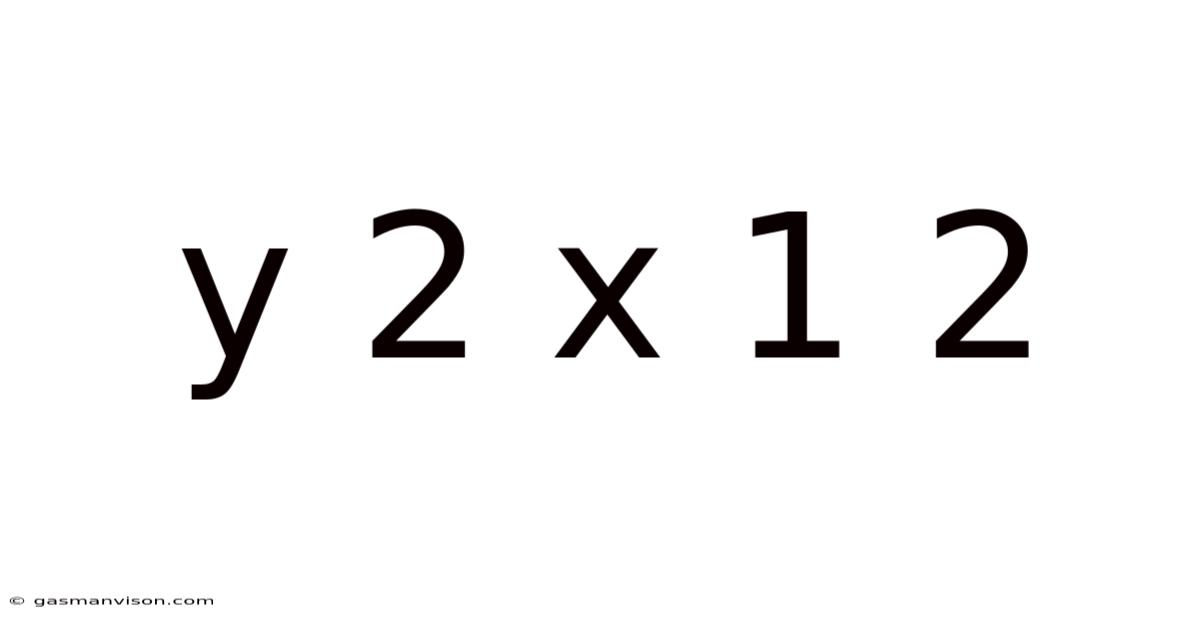
Table of Contents
Decoding the Enigma: A Deep Dive into "Y = 2X + 12"
This seemingly simple equation, Y = 2X + 12, hides a wealth of mathematical concepts and practical applications. At first glance, it appears straightforward – a linear equation representing a straight line on a graph. However, a deeper exploration reveals its significance in various fields, from basic algebra to advanced calculus and real-world modeling. This article will dissect the equation, exploring its properties, graphing techniques, practical applications, and related mathematical concepts. We'll delve into its meaning, interpretations, and how to solve problems using this foundational equation.
Understanding the Fundamentals: Linear Equations and Slope-Intercept Form
The equation Y = 2X + 12 is a classic example of a linear equation in slope-intercept form. This form, often written as Y = mX + b, provides a clear and concise way to understand the characteristics of a line. Let's break down the components:
- Y: Represents the dependent variable. Its value depends on the value of X.
- X: Represents the independent variable. We can choose any value for X, and the equation will provide the corresponding value of Y.
- m: Represents the slope of the line. The slope indicates the steepness and direction of the line. A positive slope means the line rises from left to right, while a negative slope means it falls. In our equation, m = 2, indicating a positive slope. This means for every 1 unit increase in X, Y increases by 2 units.
- b: Represents the y-intercept. This is the point where the line intersects the y-axis (where X = 0). In our equation, b = 12, meaning the line crosses the y-axis at the point (0, 12).
Graphing the Equation: Visualizing the Linear Relationship
Visualizing the equation on a graph provides a powerful understanding of its behavior. To graph Y = 2X + 12, we can use the slope-intercept form directly:
-
Plot the y-intercept: Start by plotting the point (0, 12) on the y-axis.
-
Use the slope to find additional points: Since the slope is 2 (or 2/1), we can move 1 unit to the right and 2 units up from the y-intercept to find another point on the line (1, 14). We can repeat this process to find more points, such as (2, 16), (3, 18), and so on. Alternatively, we can move 1 unit to the left and 2 units down from the y-intercept to find points like (-1, 10), (-2, 8), etc.
-
Draw the line: Connect the points with a straight line. This line represents all the possible (X, Y) pairs that satisfy the equation Y = 2X + 12.
Solving for X and Y: Finding Specific Points on the Line
The equation can be used to find the value of Y given a value of X, or vice versa.
-
Finding Y given X: Suppose we want to find the value of Y when X = 5. We substitute X = 5 into the equation: Y = 2(5) + 12 = 22. Therefore, the point (5, 22) lies on the line.
-
Finding X given Y: Suppose we want to find the value of X when Y = 20. We substitute Y = 20 into the equation: 20 = 2X + 12. Subtracting 12 from both sides gives 8 = 2X. Dividing both sides by 2 gives X = 4. Therefore, the point (4, 20) lies on the line.
Applications of Linear Equations in Real-World Scenarios
Linear equations like Y = 2X + 12 have countless real-world applications. Here are a few examples:
-
Cost Calculation: Imagine a company that charges a fixed setup fee of $12 and $2 per unit produced. The total cost (Y) can be represented as Y = 2X + 12, where X is the number of units produced.
-
Distance-Time Relationships: Consider a car traveling at a constant speed of 2 meters per second, starting 12 meters from a reference point. The distance (Y) from the reference point after X seconds can be modeled using the equation Y = 2X + 12.
-
Temperature Conversion: While not a direct application, linear equations are fundamental to converting between different temperature scales (e.g., Celsius to Fahrenheit).
-
Profit and Loss Analysis: In business, linear equations can model the relationship between the number of units sold and profit or loss. The equation's slope might represent profit per unit, and the y-intercept could be initial investment costs.
Expanding the Scope: Related Mathematical Concepts
Understanding Y = 2X + 12 opens doors to more advanced mathematical concepts:
-
Systems of Linear Equations: This equation can be combined with other linear equations to form a system. Solving such systems helps find the points of intersection between multiple lines.
-
Linear Inequalities: Replacing the equals sign with an inequality sign (>, <, ≥, ≤) transforms the equation into a linear inequality, defining a region on the graph rather than a single line.
-
Calculus: The slope (m = 2) represents the instantaneous rate of change of Y with respect to X. In calculus, this concept extends to finding the derivative of more complex functions.
-
Linear Programming: In operations research, linear programming uses linear equations and inequalities to optimize resource allocation problems.
Beyond the Basics: Exploring Variations and Extensions
While we've focused on Y = 2X + 12, the principles discussed apply to any linear equation in slope-intercept form. Changing the values of 'm' and 'b' alters the slope and y-intercept, resulting in different lines. Exploring these variations provides a deeper understanding of the relationship between the equation's parameters and the line's characteristics.
Advanced Applications and Interdisciplinary Connections
The seemingly simple equation Y = 2X + 12 serves as a foundation for complex modeling in various fields:
-
Physics: Linear equations describe relationships between variables in mechanics, such as velocity, acceleration, and displacement.
-
Economics: Supply and demand curves are often approximated using linear equations.
-
Engineering: Linear equations are crucial in structural analysis, circuit design, and many other engineering disciplines.
-
Computer Science: Linear algebra, based on linear equations, is fundamental to computer graphics, machine learning, and data analysis.
Conclusion: The Enduring Relevance of a Simple Equation
While seemingly simple, the equation Y = 2X + 12 encapsulates fundamental mathematical principles and possesses remarkable versatility. Its exploration provides a solid base for understanding linear equations, their graphical representation, and their widespread applications across various disciplines. From basic algebra to advanced mathematical modeling, this equation serves as a cornerstone of mathematical understanding, demonstrating the power and elegance of seemingly simple concepts. Its continued relevance underlines the importance of mastering fundamental concepts for tackling more complex mathematical challenges. This deep dive has hopefully illuminated the rich tapestry of information hidden within this simple, yet powerful, equation. Further exploration and experimentation are encouraged to fully grasp the potential of this foundational element of mathematics.
Latest Posts
Latest Posts
-
Molar Mass Of Ammonium Phosphate
Sep 14, 2025
-
X 3 2x 2 3x
Sep 14, 2025
-
Aquellos Sombreros Son Muy Elegantes
Sep 14, 2025
-
X 2 Y 2 16
Sep 14, 2025
-
34x 25 How To Solve
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Y 2 X 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.